 Môn Toán - Lớp 12
Môn Toán - Lớp 12
 30 bài tập trắc nghiệm đường tiệm cận của đồ thị hàm số mức độ vận dụng, vận dụng cao
30 bài tập trắc nghiệm đường tiệm cận của đồ thị hàm số mức độ vận dụng, vận dụng cao
Câu hỏi
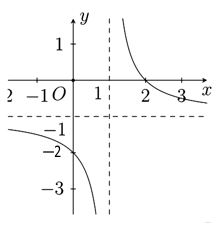
Đồ thị trong hình bên là của hàm số \(y = \dfrac{{ax + b}}{{x + c}}\)(với \(a,b,c \in \mathbb{R}\)). Khi đó tổng \(a + b + c\) bằng
- A \( - 1.\)
- B \(1\).
- C \(2\).
- D \(0\).
Phương pháp giải:
- Dựa vào đồ thị hàm số suy ra các đường tiệm cận để tìm a;c.
- Dựa vào điểm thuộc đồ thị để tìm b.
Lời giải chi tiết:
Dựa vào hàm số ta có: Đồ thị hàm số có TCN \(y = a\) và TCĐ \(x = - c\).
Dựa vào đồ thị hàm số ta có: Đồ thị hàm số có TCN \(y = - 1\) và TCĐ \(x = 1\).
\( \Rightarrow \left\{ \begin{array}{l}a = - 1\\ - c = 1\end{array} \right. \Leftrightarrow a = c = - 1\). Khi đó hàm số có dạng \(y = \dfrac{{ - x + b}}{{x - 1}}\).
Đồ thị hàm số đi qua điểm có tọa độ là \(\left( {2;0} \right) \Rightarrow 0 = \dfrac{{ - 2 + b}}{{2 - 1}} \Leftrightarrow b = 2.\)
Vậy \(a + b + c = - 1 + 2 - 1 = 0.\)
Chọn D.






