Lời giải chi tiết:

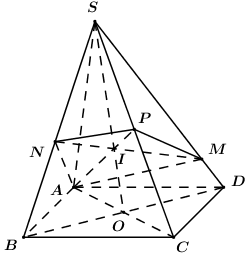
Đặt \(\dfrac{{SN}}{{SB}} = x,\,\,\dfrac{{SM}}{{SD}} = y\).

Ta có: \(\dfrac{{{V_{S.ANP}}}}{{{V_{S.ABC}}}} = \dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}} = \dfrac{1}{2}x\) \( \Rightarrow {V_{S.ANP}} = \dfrac{x}{2}{V_{S.ABC}} = \dfrac{x}{4}V\).

            \(\dfrac{{{V_{S.APM}}}}{{{V_{S.ACD}}}} = \dfrac{{SP}}{{SC}}.\dfrac{{SM}}{{SD}} = \dfrac{1}{2}y\) \( \Rightarrow {V_{S.APM}} = \dfrac{y}{2}{V_{S.ACD}} = \dfrac{y}{4}V\).

\( \Rightarrow {V_{S.AMNP}} = {V_{S.ANP}} + {V_{S.APM}} = \left( {\dfrac{x}{4} + \dfrac{y}{4}} \right)V\).

Tương tự ta có:

\(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABD}}}} = \dfrac{{SN}}{{SB}}.\dfrac{{SM}}{{SD}} = xy\) \( \Rightarrow {V_{S.AMN}} = xy{V_{S.ABD}} = \dfrac{{xy}}{2}V\).

\(\dfrac{{{V_{S.NPM}}}}{{{V_{S.BCD}}}} = \dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}}.\dfrac{{SM}}{{SD}} = \dfrac{1}{2}xy\) \( \Rightarrow {V_{S.NPM}} = \dfrac{1}{2}xy{V_{S.BCD}} = \dfrac{{xy}}{4}V\).

\( \Rightarrow {V_{S.AMNP}} = {V_{S.AMN}} + {V_{S.NPM}} = \left( {\dfrac{{xy}}{2} + \dfrac{{xy}}{4}} \right)V = \dfrac{{3xy}}{4}V\).

Khi đó ta có: \(\dfrac{x}{4} + \dfrac{y}{4} = \dfrac{{3xy}}{4} \Leftrightarrow x + y = 3xy\) \( \Leftrightarrow x\left( {3y - 1} \right) = y\).

Do \(x,\,\,y > 0\) nên \(3y - 1 > 0 \Leftrightarrow y > \dfrac{1}{3}\), khi đó ta có \(x = \dfrac{y}{{3y - 1}}\,\,\left( {y > \dfrac{1}{3}} \right)\).

Ta có \(\dfrac{{V'}}{V} = \dfrac{{x + y}}{4} = \dfrac{1}{4}\left( {\dfrac{y}{{3y - 1}} + y} \right) = \dfrac{1}{4}.\dfrac{{3{y^2}}}{{3y - 1}}\,\,\left( {y > \dfrac{1}{3}} \right)\).

Xét hàm số \(f\left( y \right) = \dfrac{{3{y^2}}}{{3y - 1}}\) ta có

\(\begin{array}{l}f'\left( y \right) = \dfrac{{6y\left( {3y - 1} \right) - 3{y^2}.3}}{{{{\left( {3y - 1} \right)}^2}}}\\f'\left( y \right) = \dfrac{{9{y^2} - 6y}}{{{{\left( {3y - 1} \right)}^2}}}\\f'\left( y \right) = 0 \Leftrightarrow \left[ \begin{array}{l}y = 0\\y = \dfrac{2}{3}\end{array} \right.\end{array}\)

BBT:

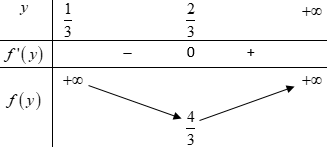
Từ BBT ta thấy \(f\left( y \right)\) đạt GTNN bằng \(\dfrac{4}{3}\) tại \(y = \dfrac{2}{3}\).

Vậy \(\min \dfrac{{V'}}{V} = \dfrac{1}{4}.\dfrac{4}{3} = \dfrac{1}{3}\). 

Chọn B.