Câu hỏi
Cho hình nón có góc ở đỉnh bằng \({60^0}\), bán kính đáy bằng a. Diện tích toàn phần hình nón đó là:
- A \(\pi {a^2}\)
- B \(3\pi {a^2}\)
- C \(2\pi {a^2}\)
- D \(\sqrt 3 \pi {a^2}\)
Phương pháp giải:
- Xác định độ dài đường sinh của hình nón.
- Sử dụng công thức tính diện tích toàn phần của hình nón: \({S_{tp}} = \pi rl + \pi {r^2}\) trong đó r, l lần lượt là bán kính đáy và độ dài đường sinh của hình nón.
Lời giải chi tiết:
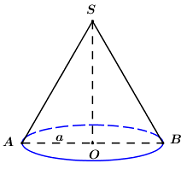
Gọi \(\Delta SAB\) là 1 thiết diện qua trục của hình nón, ta có \(\angle ASB = {60^0}\), do đó \(\Delta SAB\) đều.
Gọi O là tâm hình nón, suy ra O là trung điểm của AB và AO = r = a.
\( \Rightarrow AB = 2a \Rightarrow SA = SB = AB = 2a\) \( \Rightarrow \) Độ dài đường sinh của hình nón là \(l = 2a\).
Vậy diện tích toàn phần của hình nón là: \({S_{tp}} = \pi rl + \pi {r^2} = \pi .a.2a + \pi .{a^2} = 3\pi {a^2}\).
Chọn B.
Câu hỏi trước
