Câu hỏi
Trong không gian, cho tam giác \(ABC\) vuông tại A, \(AB = a\) và \(\widehat {ABC} = {60^0}\). Tính độ dài đường sinh \(l\) của hình nón, nhận được khi quay tam giác \(ABC\) xung quanh trục \(AC\).
- A \(l = \sqrt 2 a\).
- B \(l = a\).
- C \(l = \sqrt 3 a\).
- D \(l = 2a\)
Phương pháp giải:
Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.
Lời giải chi tiết:
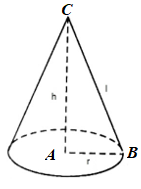
Khi quay tam giác vuông ABC quanh cạnh AC ta được hình nón có đường sinh \(l = BC\), bán kính đáy \(r = AB\).
Hình nón nhận được khi quay tam giác \(ABC\) xung quanh trục \(AC\) có độ dài đường sinh là:
\(l = BC = \dfrac{{AB}}{{\cos \angle ABC}} = \dfrac{a}{{\cos {{60}^0}}} = \dfrac{a}{{\dfrac{1}{2}}} = 2a\).
Chọn D.
Câu hỏi trước
