Câu hỏi
Cho tam giác \(ABC\) vuông tại \(A\). Giải tam giác vuông trong các trường hợp sau:
Câu 1:
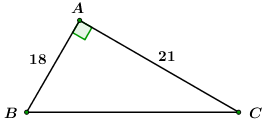
\(AB{\rm{ }} = {\rm{ 18}}cm;AC = 21cm\)
- A \(BC = 3\sqrt {85} \,\,;\,\,\angle B = {59^0}\,\,;\,\,\angle C = {31^0}\)
- B \(BC = 3\sqrt {85} \,\,;\,\,\angle B = {31^0}\,\,;\,\,\angle C = {59^0}\)
- C \(BC = 3\sqrt {85} \,\,;\,\,\angle B = {40^0}36'\,\,;\,\,\angle C = {49^0}24'\)
- D \(BC = 3\sqrt {85} \,\,;\,\,\angle B = {49^0}24'\,\,;\,\,\angle C = {40^0}36'\)
Phương pháp giải:
Sử dụng định lý Pitago cho tam giác ABC vuông tại A để tính độ dài cạnh BC.
Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông
Sử dụng tính chất hai góc phụ nhau
Lời giải chi tiết:
\(AB = {\rm{18}}cm;\,\,\,AC = 21cm\)
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {18^2} + {21^2} = 765\)\( \Rightarrow BC = 3\sqrt {85} \)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \frac{{AC}}{{BC}} = \frac{{21}}{{3\sqrt {85} }} \Rightarrow \angle B \approx {49^0}24'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có: \(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {49^0}24' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {40^0}36'\)
Chọn D.
Câu 2:
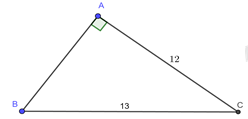
\(AC{\rm{ }} = {\rm{ 12}}cm;CB = 13cm\)
- A \(AB = 5cm\,\,;\,\,\angle B = {22^0}37'\,\,;\,\,\angle C = {67^0}23'\)
- B \(AB = 5cm\,\,;\,\,\angle B = {67^0}23'\,\,;\,\,\angle C = {22^0}37'\)
- C \(AB = 5cm\,\,;\,\,\angle B = {24^0}37'\,\,;\,\,\angle C = {65^0}23'\)
- D \(AB = 5cm\,\,;\,\,\angle B = {65^0}23'\,\,;\,\,\angle C = {24^0}37'\)
Phương pháp giải:
Sử dụng định lý Pitago cho tam giác ABC vuông tại A để tính độ dài cạnh BC.
Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông
Sử dụng tính chất hai góc phụ nhau
Lời giải chi tiết:
\(AC = {\rm{12}}cm;\,\,\,CB = 13cm\)
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow A{B^2} = {13^2} - {12^2} = 25\)\( \Rightarrow BA = 5\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \frac{{AC}}{{BC}} = \frac{{12}}{{13}} \Rightarrow \angle B \approx {67^0}23'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {67^0}23' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {22^0}37'\)
Chọn A.