Câu hỏi
Cho tam giác \(ABC\) vuông tại \(A\). Giải tam giác vuông trong các trường hợp sau:
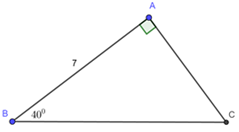
Câu 1:
\(\angle B = {40^0}\)và \(AB{\rm{ }} = {\rm{ 7}}\)
- A \(AC = 8,34\,\,;\,\,BC = 10,89\,\,;\,\,\angle C = {50^0}\)
- B \(AC = 4,5\,\,;\,\,BC = 9,14\,\,;\,\,\angle C = {50^0}\)
- C \(AC = 5,87\,\,;\,\,BC = 9,14\,\,;\,\,\angle C = {50^0}\)
- D \(AB = 4,5\,\,;\,\,AC = 10,89\,\,;\,\,\angle C = {50^0}\)
Phương pháp giải:
Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông.
Sử dụng tính chất hai góc phụ nhau: Cho \(\angle B + \angle C = {90^0}.\) Khi đó ta có: \(\left\{ \begin{array}{l}\sin B = \cos C\\\cos B = \sin C\end{array} \right..\)
Lời giải chi tiết:
\(\angle B = {40^0}\) và \(AB = {\rm{7}}{\rm{.}}\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(AC = AB.tanB = 7.\tan {40^0} \approx 5,87\)
\(AB = BC.\cos B \Rightarrow 7 = BC.\cos {40^0}\)\( \Rightarrow BC = \frac{7}{{\cos {{40}^0}}} \approx 9,14\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {40^0} + \angle C = {90^0}\)\( \Leftrightarrow \angle C = {50^0}\)
Chọn C.
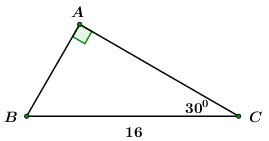
Câu 2:
\(\angle C = {30^0}\) và \(BC{\rm{ }} = {\rm{ 16}}\)
- A \(AB = 8\,\,;\,\,AC = 8\sqrt 3 \,\,;\,\,\angle B = {60^0}\)
- B \(AB = 8\sqrt 3 \,\,;\,\,AC = 8\,\,;\,\,\angle B = {60^0}\)
- C \(AB = \frac{{16\sqrt 3 }}{3}\,\,;\,\,AC = \frac{{16\sqrt 6 }}{3}\,\,;\,\,\angle B = {60^0}\)
- D \(AB = \frac{{16\sqrt 6 }}{3}\,\,;\,\,AC = \frac{{16\sqrt 3 \,}}{3}\,;\,\,\angle B = {60^0}\)
Phương pháp giải:
Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông.
Sử dụng tính chất hai góc phụ nhau: Cho \(\angle B + \angle C = {90^0}.\) Khi đó ta có: \(\left\{ \begin{array}{l}\sin B = \cos C\\\cos B = \sin C\end{array} \right..\)
Lời giải chi tiết:
\(\angle C = {30^0}\) và \(BC = {\rm{16}}{\rm{.}}\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(AC = BC.cosC = 16.cos{30^0} = 8\sqrt 3 \)
\(AB = BC.\sin C = 16.\sin {30^0} = 8\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow \angle B + {30^0} = {90^0}\)\( \Leftrightarrow \angle B = {60^0}\)
Chọn A.