Câu hỏi
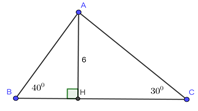
Cho tam giác ABC, \(\angle B = {40^0};\angle C = {30^0}\), đường cao \(AH{\rm{ }} = {\rm{ 6}}cm\). Tính AB, AC và BC.
- A \(AB = 8,26\,\,;\,\,\,AC = 10\,\,;\,\,BC = 6,65 + 6\sqrt 2 \)
- B \(AB = 9,33\,\,;\,\,\,AC = 10\,\,;\,\,BC = 7,15 + 6\sqrt 2 \)
- C \(AB = 8,26\,;\,\,\,AC = 12\,\,;\,\,BC = 6,65 + 6\sqrt 3 \)
- D \(AB = 9,33\,\,;\,\,\,AC = 12\,\,;\,\,BC = 7,15 + 6\sqrt 3 \)
Phương pháp giải:
Sử dụng tính chất cộng đoạn thẳng.
Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông.
Lời giải chi tiết:
Xét \(\Delta ABH\) vuông tại \(H\) ta có :
\(AH = AB.sinB\) \( \Rightarrow AB = \frac{{AH}}{{sinB}} = \frac{6}{{sin{{40}^0}}} \approx 9,33\)
\(HB = AH.cotB = 6.cot{40^0} \approx 7,15\)
Xét \(\Delta ACH\) vuông tại \(H\) ta có:
\(AH = AC.\sin C\) \( \Rightarrow AC = \frac{{AH}}{{\sin C}} = \frac{6}{{sin{{30}^0}}} = 12\)
\(HC = AH.cotC = 6.cot{30^0} = 6\sqrt 3 \)
Ta có: \(BC = HB + HC \approx 7,15 + 6\sqrt 3 \)
Chọn D.