Phương pháp giải:

Sử dụng giản đồ vecto.

Hệ số công suất của đoạn mạch: \(\cos \varphi  = \dfrac{R}{Z}\)

Lời giải chi tiết:

+ Ta có giản đồ vecto:

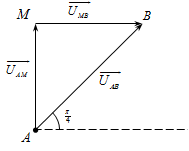
Hệ số công suất của đoạn mạch:

\(\cos \varphi  = \dfrac{{\sqrt 2 }}{2} \Rightarrow \varphi  = \dfrac{\pi }{4} \Rightarrow \) \(\Delta AMB\) vuông cân tại \(M\)

\( \Rightarrow {U_{0AM}} = {U_{0MB}} = \dfrac{{{U_0}}}{{\sqrt 2 }} = \dfrac{{80\sqrt 2 }}{{\sqrt 2 }} = 80V\)

+ Lại có \({u_{AM}}\)vuông pha với \({u_{MB}}\)

\(\begin{array}{l} \Rightarrow {\left( {\dfrac{{{u_{AM}}}}{{{U_{0AM}}}}} \right)^2} + {\left( {\dfrac{{{u_{MB}}}}{{{U_{0MB}}}}} \right)^2} = 1\\ \Rightarrow u_{MB}^2 = \sqrt {U_{0AM}^2 - u_{AM}^2}  = \sqrt {{{80}^2} - {{48}^2}}  = 64V\end{array}\)

Chọn A.