Phương pháp giải:

Tần số góc của con lắc: \(\omega  = \sqrt {\dfrac{k}{m}} \)

Sử dụng vòng tròn lượng giác và công thức: \(\Delta \varphi  = \omega .\Delta t\)

Giữ lò xo: \(k'x' = kx\)

Công thức độc lập với thời gian: \({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)

Lời giải chi tiết:

Tần số góc của con lắc là: \(\omega  = \sqrt {\dfrac{k}{m}}  = \sqrt {\dfrac{{40}}{{0,4}}}  = 10\,\,\left( {rad/s} \right)\)

Trong thời gian \(\dfrac{{7\pi }}{{30}}\,\,s\), vecto quay được góc:

\(\Delta \varphi  = \omega .\Delta t = 10.\dfrac{{7\pi }}{{30}} = \dfrac{{7\pi }}{3} = 2\pi  + \dfrac{\pi }{3}\,\,\left( {rad} \right)\)

Ta có vòng trong lượng giác:

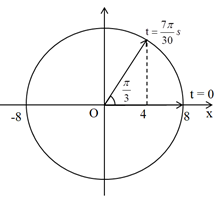
Từ vòng tròn lượng giác ta thấy tại thời điểm \(\dfrac{{7\pi }}{{30}}\,\,s\), vật có li độ \(x = 4\,\,cm\)

Áp dụng công thức độc lập với thời gian ta có:

\({x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow v = \omega .\sqrt {{A^2} - {x^2}}  = 10.\sqrt {{8^2} - {4^2}}  = 40\sqrt 3 \,\,\left( {cm/s} \right)\)

Giữ điểm chính giữa lò xo, li độ mới của vật tại điểm giữ là: \(x' = \dfrac{x}{2} = 2\,\,\left( {cm} \right)\)

Độ cứng của lò xo khi đó: \(k'x' = kx \Rightarrow k' = \dfrac{{kx}}{{x'}} = 2k = 80\,\,\left( {N/m} \right)\)

Tần số góc của con lắc mới là: \(\omega ' = \sqrt {\dfrac{{k'}}{m}}  = \sqrt {\dfrac{{80}}{{0,4}}}  = 10\sqrt 2 \,\,\left( {rad/s} \right)\)

Giữ lò xo, vận tốc của vật không thay đổi. Áp dụng công thức độc lập với thời gian, ta có:

\(x{'^2} + \dfrac{{{v^2}}}{{\omega {'^2}}} = A{'^2} \Rightarrow {2^2} + \dfrac{{{{\left( {40\sqrt 3 } \right)}^2}}}{{{{\left( {10\sqrt 2 } \right)}^2}}} = A{'^2} \Rightarrow A' = 2\sqrt 7 \,\,\left( {cm} \right)\)

Chọn C.