Phương pháp giải:

Điều kiện cân bằng của vật: \(\sum {\overrightarrow F  = \overrightarrow 0 } \)

Lời giải chi tiết:

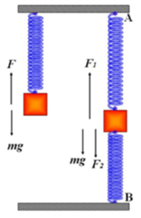
Khi treo lò xo vào điểm A, vật ở VTCB, ta có:

\(\overrightarrow F  + \overrightarrow P  = \overrightarrow 0  \Rightarrow k\Delta l = mg \Rightarrow k = \dfrac{{mg}}{{\Delta l}} = \dfrac{{0,2.10}}{{0,08}} = 25\,\,\left( {N/m} \right)\)

Khi mắc 2 lò xo vào hai điểm A, B, vật ở VTCB, ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}AB = {l_1} + {l_2}\\\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow P  = \overrightarrow 0 \end{array} \right. \Rightarrow \left\{ \begin{array}{l}AB = \left( {{l_0} + \Delta {l_1}} \right) + \left( {{l_0} + \Delta {l_2}} \right)\\{F_1} = P + {F_2}\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\Delta {l_1} + \Delta {l_2} = AB - 2{l_0}\\k\Delta {l_1} = mg + k\Delta {l_2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\Delta {l_1} + \Delta {l_2} = 0,12\\\Delta {l_1} - \Delta {l_2} = \dfrac{{mg}}{k} = 0,08\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}\Delta {l_1} = 0,1\,\,\left( m \right) = 10\,\,\left( {cm} \right)\\\Delta {l_2} = 0,02\,\,\left( m \right) = 2\,\,\left( {cm} \right)\end{array} \right.\end{array}\)

Vậy VTCB mới cách A đoạn: \({l_1} = {l_0} + \Delta {l_1} = 30 + 10 = 40\,\,\left( {cm} \right)\)

Chọn C.