Câu hỏi
Cho hình chóp \(S.ABC\) có \(AB = \sqrt 2 a\), \(AC = a\), \(BC = \sqrt 3 a\), \(\angle SBA = \angle SCA = {90^0}\). Và hai mặt phẳng (SAB) và (SAC) tạo với nhau một góc \(\alpha \) sao cho \(\cos \alpha = \dfrac{1}{{\sqrt 3 }}\). Thể tích khối chóp \(S.ABC\) bằng:
- A \(\dfrac{{\sqrt 2 {a^3}}}{{12}}\)
- B \(\dfrac{{\sqrt 2 {a^3}}}{2}\)
- C \(\dfrac{{\sqrt 2 {a^3}}}{3}\)
- D \(\dfrac{{\sqrt 2 {a^3}}}{6}\)
Lời giải chi tiết:
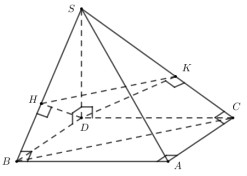
Từ giả thiết: \(AB = \sqrt 2 a,\,\,AC = a,\,\,BC = \sqrt 3 a\) \( \Rightarrow B{C^2} = 3{a^2} = 2{a^2} + {a^2} = A{B^2} + A{C^2}\) \( \Rightarrow \Delta ABC\) vuông tại A.
Dựng \(SD \bot \left( {ABC} \right) \Rightarrow ABDC\) là hình chữ nhật.
Ta có: \(DB = AC = a,\,\,DC = AB = \sqrt 2 a\).
Đặt \(SD = h\). Áp dụng công thức tính nhanh ta có: \(\dfrac{{DB}}{{SB}}.\dfrac{{DC}}{{SC}} = \cos \alpha \).
Coi \(a = 1\), ta có:
\(\begin{array}{l}\dfrac{1}{{\sqrt {{h^2} + 1} }}.\dfrac{{\sqrt 2 }}{{\sqrt {{h^2} + 2} }} = \dfrac{1}{{\sqrt 3 }} \Leftrightarrow {h^4} + 3{h^2} - 4 = 0\\ \Leftrightarrow {h^2} = 1 \Leftrightarrow h = 1 \Rightarrow h = a = SD\end{array}\)
Vậy \({V_{S.ABC}} = \dfrac{1}{3}SD.{S_{ABC}} = \dfrac{1}{3}SD.\dfrac{1}{2}AB.AC = \dfrac{{\sqrt 2 {a^3}}}{6}\).
Chọn D.







