Câu hỏi
Cho tứ diện MNPQ có MQ vuông góc với mặt phẳng \(\left( {MNP} \right)\),\(MP = MQ = 3,\) \(MN = 4,\) \(NP = 5\). Khoảng cách từ M đến mặt phẳng \(\left( {NPQ} \right)\) bằng
- A \(\dfrac{{6\sqrt {41} }}{{41}}\)
- B \(\dfrac{{4\sqrt {41} }}{{41}}\)
- C \(\dfrac{{24\sqrt {41} }}{{41}}\)
- D \(\dfrac{{12\sqrt {41} }}{{41}}\)
Phương pháp giải:
- Chứng minh tam giác MNP vuông và tính độ dài đường cao kẻ từ M xuống NP.
- Áp dụng hệ thức lượng trong tam giác vuông để tìm khoảng cách từ M đến \(\left( {NPQ} \right)\).
Lời giải chi tiết:
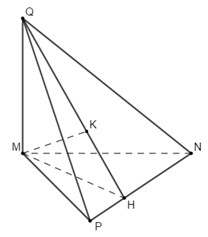
Ta có \(MP = 3;MN = 4;NP = 5 \Rightarrow N{P^2} = M{N^2} + M{P^2}\) nên tam giác MNP vuông tại M.
Kẻ \(MH \bot NP \Rightarrow \dfrac{1}{{M{H^2}}} = \dfrac{1}{{M{P^2}}} + \dfrac{1}{{M{N^2}}} \Rightarrow MH = \dfrac{{12}}{5}\)
Mà \(MQ \bot \left( {MNP} \right) \Rightarrow MQ \bot NP;MH \bot NP \Rightarrow \) từ M kẻ \(MK \bot QH \Rightarrow {d_{\left( {M;\left( {NQP} \right)} \right)}} = MK\)
Ta có \(\dfrac{1}{{M{K^2}}} = \dfrac{1}{{M{Q^2}}} + \dfrac{1}{{M{H^2}}} \Rightarrow MK = \dfrac{{12\sqrt {41} }}{{41}}\)
Chọn D.







