Câu hỏi
Cho số phức z thỏa mãn \(\dfrac{{\left( { - 1 + i} \right)z + 2}}{{1 - 2i}} = 2 + 3i\). Số phức liên hợp của z là \(\overline z = a + bi\) với \(a,\,\,b \in \mathbb{R}\). Giá trị của \(a + b\) bằng:
- A \( - 1\).
- B \( - 12.\)
- C \( - 6\).
- D \( 1\).
Phương pháp giải:
- Tìm số phức z bằng MTCT rồi suy ra \(\overline z \): Số phức \(z = a + bi\) có số phức liên hợp \(\overline z = a - bi\).
- Xác định các hệ số \(a,\,\,b\) và tính tổng \(a + b\).
Lời giải chi tiết:
Ta có \(\dfrac{{\left( { - 1 + i} \right)z + 2}}{{1 - 2i}} = 2 + 3i \Rightarrow z = \dfrac{{\left( {2 + 3i} \right)\left( {1 - 2i} \right) - 2}}{{ - 1 + i}} = - \dfrac{7}{2} - \dfrac{5}{2}i\)
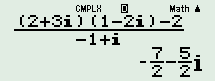
\(\begin{array}{l} \Rightarrow \overline z = - \dfrac{7}{2} + \dfrac{5}{2}i\\ \Rightarrow a = - \dfrac{7}{2};\,\,b = \dfrac{5}{2}\end{array}\)
Vậy \(a + b = - \dfrac{7}{2} + \dfrac{5}{2} = - 1.\)
Chọn A.
Câu hỏi trước
