Câu hỏi
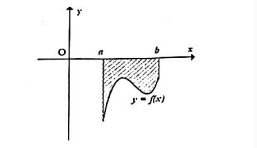
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Khi quay hình phẳng như hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích là:
- A \(\pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} .\)
- B \(\int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} .\)
- C \( - \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} .\)
- D \( - \int\limits_a^b {f\left( x \right)dx} .\)
Phương pháp giải:
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Khi quay hình phẳng như hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích là: \(V = \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} \)
Lời giải chi tiết:
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Khi quay hình phẳng như hình vẽ bên quanh trục Ox ta được khối tròn xoay có thể tích là: \(V = \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} \)
Chọn A.







