Phương pháp giải:

- Sử dụng công thức: Diện tích hình phẳng phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành, đường thẳng \(x = a,\,\,x = b\) là \(\int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).

- Tính tích phân theo \(m\) và tìm GTNN của biểu thức.

Lời giải chi tiết:

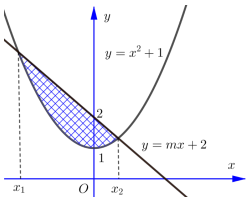
Ta có \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \( - {x^2} + mx + 1 = 0\).

Khi đó ta có:

\(\begin{array}{l}S = \int\limits_{{x_1}}^{{x_2}} {\left( {mx + 2 - {x^2} - 1} \right)dx} \\\,\,\,\, = \left. {\left( {\dfrac{{m{x^2}}}{2} + 2x - \dfrac{{{x^3}}}{3} - x} \right)} \right|_{{x_1}}^{{x_2}}\\\,\,\,\, = \left( {\dfrac{{mx_2^2}}{2} + 2{x_2} - \dfrac{{x_2^3}}{3} - {x_2}} \right) - \left( {\dfrac{{mx_1^2}}{2} + 2{x_1} - \dfrac{{x_1^3}}{3} - {x_1}} \right)\\\,\,\,\, = \dfrac{m}{2}\left( {x_2^2 - x_1^2} \right) + 2\left( {{x_2} - {x_1}} \right) - \dfrac{1}{3}\left( {x_2^3 - x_1^3} \right) - \left( {{x_2} - {x_1}} \right)\\\,\,\,\, = \left( {{x_2} - {x_1}} \right)\left[ {\dfrac{m}{2}\left( {{x_2} + {x_1}} \right) + 2 - \dfrac{1}{3}\left( {x_2^2 + {x_1}{x_2} + x_1^2} \right) - 1} \right]\\\,\,\,\, = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2}} \left[ { - \dfrac{1}{3}\left( {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2}} \right) + \dfrac{m}{2}\left( {{x_1} + {x_2}} \right) + 1} \right]\\\,\,\,\, = \sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \left[ { - \dfrac{1}{3}\left( {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2}} \right) + \dfrac{m}{2}\left( {{x_1} + {x_2}} \right) + 1} \right]\end{array}\)

Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} =  - 1\end{array} \right.\).

Suy ra

\(\begin{array}{l}S = \sqrt {{m^2} + 4} .\left[ { - \dfrac{1}{3}\left( {{m^2} + 1} \right) + \dfrac{m}{2}.m + 1} \right]\\S = \dfrac{1}{6}\sqrt {{m^2} + 4} \left( { - 2{m^2} - 2 + 3{m^2} + 6} \right)\\S = \dfrac{1}{6}\sqrt {{m^2} + 4} \left( {{m^2} + 4} \right) \ge \dfrac{1}{6}.\sqrt 4 .4 = \dfrac{4}{3}\end{array}\)

Dấu “=” xảy ra \( \Leftrightarrow m = 0\).

Chọn A.