Phương pháp giải:

- Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Tính độ dài đường cao và cạnh đáy tương ứng của tam giác \(IBC\), từ đó tính diện tích tam giác.

Lời giải chi tiết:

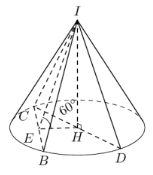
Gọi thiết diện qua trục của hình nón là \(\Delta ICD\).

\(\Delta ICD\) vuông cân tại \(I\) có cạnh huyền \(CD = a\sqrt 2  \Rightarrow IC = ID = a\) và \(IH = \dfrac{1}{2}CD = \dfrac{{a\sqrt 2 }}{2}\).

Gọi \(E\) là trung điểm của \(BC\), gọi \(H\) là đường đường tròn đáy của hình nón ta có \(\left\{ \begin{array}{l}BC \bot IE\\BC \bot HE\end{array} \right.\).

\( \Rightarrow \angle \left( {\left( {IBC} \right);\left( {HBC} \right)} \right) = \angle \left( {IE;HE} \right) = \angle IEH = {60^0}\).

Xét \({\Delta _v}IHE\) có \(IE = \dfrac{{IE}}{{\sin {{60}^0}}} = \dfrac{{a\sqrt 2 }}{2}:\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 2 }}{{\sqrt 3 }}\).

                       \(HE = IH.\cot {60^0} = \dfrac{{a\sqrt 2 }}{{2\sqrt 3 }}\).

Áp dụng định lí Pytago trong tam giác vuông \(CHE\) có: \(CE = \sqrt {C{H^2} - H{E^2}}  = \dfrac{{a\sqrt 3 }}{3}\)\( \Rightarrow BC = \dfrac{{2a\sqrt 3 }}{3}\).

Vậy \({S_{\Delta IBC}} = \dfrac{1}{2}IE.BC = \dfrac{1}{2}.\dfrac{{a\sqrt 2 }}{{\sqrt 3 }}.\dfrac{{2a\sqrt 3 }}{3} = \dfrac{{{a^2}\sqrt 2 }}{3}\).

Chọn C.