Câu hỏi
Cho một hình trụ tròn xoay và hình vuông \(ABCD\) cạnh \(a\) có hai đỉnh liên tiếp \(A,\,\,B\) nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng \(ABCD\) tạo với đáy hình trụ góc \({45^0}\). Tính diện tích xung quanh hình trụ?
- A \({S_{xq}} = \dfrac{{2\pi {a^2}\sqrt 3 }}{5}\)
- B \({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 3 }}{3}\)
- C \({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 3 }}{4}\)
- D \({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 3 }}{2}\)
Phương pháp giải:
- Gọi \(P,\,\,Q,\,\,E\) lần lượt là trung điểm của \(AB,\,\,CD,\,\,OO'\). Xác định góc giữa \(\left( {ABCD} \right)\) và mặt đáy.
- Sử dụng tỉ số lượng giác và định lí Pytago tính chiều cao \(h\) và bán kính đáy \(r\) của hình trụ.
- Diện tích xung quanh của hình trụ có chiều cao \(h\) và bán kính đáy \(r\) là \({S_{xq}} = 2\pi rh\).
Lời giải chi tiết:
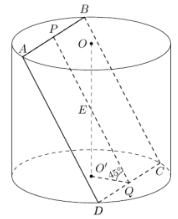
Gọi \(P,\,\,Q,\,\,E\) lần lượt là trung điểm của \(AB,\,\,CD,\,\,OO'\).
Dễ thấy góc giữa \(\left( {ABCD} \right)\) và mặt đáy là \(\angle O'QE = {45^0}\).
Ta có: \(EQ = \dfrac{1}{2}BC = \dfrac{a}{2}\), tam giác \(O'EQ\) vuông cân tại \(O'\) nên \(O'Q = O'E = \dfrac{{EQ}}{{\sqrt 2 }} = \dfrac{a}{{2\sqrt 2 }}\).
\( \Rightarrow OO' = 2O'E = \dfrac{a}{{\sqrt 2 }}\), bán kính mặt trụ là: \(r = O'C = \sqrt {O'{Q^2} + Q{C^2}} = \sqrt {{{\left( {\dfrac{a}{{2\sqrt 2 }}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 6 }}{4}\).
Vậy diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .\dfrac{{a\sqrt 6 }}{4}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{\pi {a^2}\sqrt 3 }}{2}\).
Chọn D.







