Lời giải chi tiết:

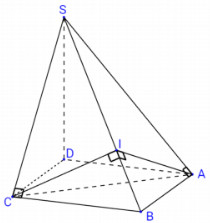
Trong \(\left( {SAB} \right)\) kẻ \(AI \bot SB\,\,\left( {I \in SC} \right)\). Nối \(CI\).

Xét \(\Delta SAB\) và \(\Delta SCB\) có:

\(\angle SAB = \angle SCB = {90^0}\), \(SB\) chung, \(AB = CB\).

\( \Rightarrow \Delta SAB = \Delta SCB\) (cạnh huyền – cạnh góc vuông)

\( \Rightarrow \angle SBA = \angle SBC\) (2 góc tương ứng).

Xét \(\Delta ABI\) và \(\Delta CBI\) có:

\(BI\) chung, \(\angle ABI = \angle CBI\,\,\left( {cmt} \right)\), \(AB = CB\,\,\left( {gt} \right)\).

\( \Rightarrow \Delta ABI = \Delta CBI\,\,\left( {c.g.c} \right)\)

\( \Rightarrow \angle BIC = \angle BIA = {90^0} \Rightarrow CI \bot SB\).

Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SBC} \right) = SB\\\left( {SAB} \right) \supset AI \bot SB\\\left( {SBC} \right) \supset CI \bot SB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {SBC} \right)} \right) = \angle \left( {AI;CI} \right) = \alpha \).

\( \Rightarrow \cos \alpha  = \dfrac{9}{{16}}\) nếu \(\alpha \) là góc nhọn hoặc \(\cos \alpha  =  - \dfrac{9}{{16}}\) nếu \(\alpha \) là góc tù.

Vì tam giác \(ABC\) vuông cân tại \(B\) có \(BA = BC = 5a\) nên \(AC = 5a\sqrt 2 \).

TH1: \(\cos \alpha  = \dfrac{9}{{16}}\), áp dụng định lí Cosin trong tam giác ACI ta có:

\(\begin{array}{l}\cos \alpha  = \dfrac{{A{I^2} + C{I^2} - A{C^2}}}{{2AI.CI}}\\ \Leftrightarrow \dfrac{9}{{16}} = \dfrac{{2A{I^2} - 50{a^2}}}{{2A{I^2}}}\\ \Leftrightarrow 18A{I^2} = 32A{I^2} - 800{a^2}\end{array}\)

\( \Leftrightarrow A{I^2} = \dfrac{{400}}{7}{a^2} \Rightarrow AI = \dfrac{{20a}}{{\sqrt 7 }} > AB\)  (vô lí vì \(AI < AB\)).

TH2: \(\cos \alpha  = \dfrac{{ - 9}}{{16}}\), áp dụng định lí Cosin trong tam giác ACI ta có:

\(\begin{array}{l}\cos \alpha  = \dfrac{{A{I^2} + C{I^2} - A{C^2}}}{{2AI.CI}}\\ \Leftrightarrow  - \dfrac{9}{{16}} = \dfrac{{2A{I^2} - 50{a^2}}}{{2A{I^2}}}\\ \Leftrightarrow  - 18A{I^2} = 32A{I^2} - 800{a^2}\\ \Leftrightarrow A{I^2} = 16{a^2} \Leftrightarrow AI = 4a = CI\end{array}\)

Dựng \(SD \bot \left( {ABC} \right)\) tại \(D\), ta có: \(\left\{ \begin{array}{l}BA \bot SA\\BD \bot SD\end{array} \right. \Rightarrow BA \bot \left( {SAD} \right)\) \( \Rightarrow BA \bot AD\).

Chứng minh tương tự ta có \(BC \bot CD\), do đó tứ giác \(ABCD\) là hình vuông.

\( \Rightarrow AC = BD = 5\sqrt 2 a\).

Áp dụng định lí Pytago trong tam giác vuông \(SBD\) ta có: \(SD = \sqrt {S{B^2} - B{D^2}}  = \dfrac{{5\sqrt 7 a}}{3}\).

\({S_{ABC}} = \dfrac{1}{2}BA.BC = \dfrac{1}{2}.5a.5a = \dfrac{{25{a^2}}}{2}\).

Vậy \({V_{S.ABC}} = \dfrac{1}{3}.SD.{S_{\Delta ABC}} = \dfrac{1}{3}.\dfrac{{5\sqrt 7 a}}{3}.\dfrac{{25{a^2}}}{2} = \dfrac{{125\sqrt 7 {a^3}}}{{18}}\).

Chọn C.