Phương pháp giải:

- Tìm \(F\left( x \right) = \int {f\left( x \right)dx} \) bằng nguyên hàm cơ bản \(\int {\dfrac{1}{{{{\sin }^2}x}}dx}  =  - \cot x + C\) và phương pháp đổi biến số.

- Khảo sát, lập BBT và tìm GTLN của hàm số \(F\left( x \right)\).

- Giải phương trình \(\mathop {\max }\limits_{\left( {0;3} \right)} F\left( x \right) = \sqrt 3 \) tìm \(C\), suy ra hàm số \(F\left( x \right)\) hoàn chỉnh.

- Tính các đáp án và chọn đáp án đúng.

Lời giải chi tiết:

Ta có: \(F\left( x \right) = \int {f\left( x \right)dx}  = \int {\dfrac{{2\cos x - 1}}{{{{\sin }^2}x}}dx} \) \( = 2\int {\dfrac{{\cos x}}{{{{\sin }^2}x}}dx}  - \int {\dfrac{1}{{{{\sin }^2}x}}dx} \)\( = 2{I_1} + \cot x + C\).

Đặt \(t = \sin x \Leftrightarrow dt = \cos dx\).

Khi đó ta có: \({I_1} = \int {\dfrac{{dt}}{{{t^2}}}}  =  - \dfrac{1}{t} + C = \dfrac{{ - 1}}{{\sin x}} + C\).

Do đó \(F\left( x \right) = \int {f\left( x \right)dx}  =  - \dfrac{2}{{\sin x}} + \cot x + C\).

Ta có: \(F'\left( x \right) = \dfrac{{2\cos x}}{{{{\sin }^2}x}} - \dfrac{1}{{{{\sin }^2}x}} = \dfrac{{2\cos x - 1}}{{{{\sin }^2}x}}\).

Cho \(F'\left( x \right) = 0 \Leftrightarrow 2\cos x - 1 = 0 \Leftrightarrow \cos x = \dfrac{1}{2}\) \( \Leftrightarrow x =  \pm \dfrac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\).

Mà \(\) nên \(x = \dfrac{\pi }{3}\). Ta có BBT như sau:

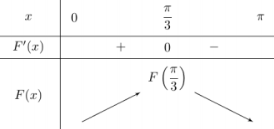
Dựa vào BBT ta thấy hàm số \(F\left( x \right)\) đạt GTLN tại \(x = \dfrac{\pi }{3}\).

\( \Rightarrow F\left( {\dfrac{\pi }{3}} \right) = \sqrt 3  \Leftrightarrow \dfrac{{ - 2}}{{\sin \dfrac{\pi }{3}}} + \cot \dfrac{\pi }{3} + C = \sqrt 3 \) \( \Leftrightarrow  - \dfrac{{4\sqrt 3 }}{3} + \dfrac{{\sqrt 3 }}{3} + C = \sqrt 3 \) \( \Leftrightarrow C = 2\sqrt 3 \).

\( \Rightarrow F\left( x \right) =  - \dfrac{2}{{\sin x}} + \cot x + 2\sqrt 3 \).

Vậy \(F\left( {\dfrac{\pi }{6}} \right) =  - \dfrac{2}{{\sin \dfrac{\pi }{6}}} + \cot \dfrac{\pi }{6} + 2\sqrt 3 \) \( =  - 4 + \sqrt 3  + 2\sqrt 3  = 3\sqrt 3  - 4\).

Chọn A.