Câu hỏi
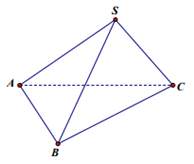
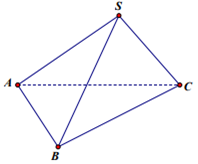
Cho hình chóp \(S.ABC\) có \(BC = a\sqrt 2 \), các cạnh còn lại đều bằng \(a\). Góc giữa hai vecto \(\overrightarrow {SB} \) và \(\overrightarrow {AC} \) bằng:
- A \(60^\circ .\)
- B \(30^\circ .\)
- C \(90^\circ .\)
- D \(120^\circ .\)
Phương pháp giải:
- Tính tích vô hướng \(\overrightarrow {SB} .\overrightarrow {AC} \).
- Sử dụng định nghĩa tích vô hướng \(\overrightarrow {SB} .\overrightarrow {AC} = SB.AC.\cos \left( {\overrightarrow {SB} ;\overrightarrow {AC} } \right)\).
Lời giải chi tiết:
Ta có
\(\begin{array}{l}\overrightarrow {SB} .\overrightarrow {AC} = \left( {\overrightarrow {SC} + \overrightarrow {CB} } \right).\overrightarrow {AC} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {SC} .\overrightarrow {AC} + \overrightarrow {CB} .\overrightarrow {AC} \end{array}\)
+) \(\overrightarrow {SC} .\overrightarrow {AC} = SC.AC.cos\angle \left( {\overrightarrow {SC} ;\overrightarrow {AC} } \right)\).
Xét \(\Delta SAC\) ta có \(SA = AC = SC = a \Rightarrow \Delta SAC\) đều \( \Rightarrow \angle \left( {\overrightarrow {SC} ;\overrightarrow {AC} } \right) = {60^0}\).
\( \Rightarrow \overrightarrow {SC} .\overrightarrow {AC} = a.a.\cos {60^0} = \frac{1}{2}{a^2}\).
+) \(\overrightarrow {CB} .\overrightarrow {AC} = CB.AC.\cos \angle \left( {\overrightarrow {CB} ;\overrightarrow {AC} } \right)\).
Xét tam giác \(ABC\) có \(AB = AC = a,\,\,BC = a\sqrt 2 \) \( \Rightarrow \Delta ABC\) vuông cân tại \(A\).
\( \Rightarrow \angle \left( {\overrightarrow {CB} ;\overrightarrow {AC} } \right) = {180^0} - {45^0} = {135^0}\).
\( \Rightarrow \overrightarrow {CB} .\overrightarrow {AC} = a\sqrt 2 .a.\cos {135^0} = - {a^2}\).
\(\begin{array}{l} \Rightarrow \overrightarrow {SB} .\overrightarrow {AC} = \frac{1}{2}{a^2} - {a^2} = - \frac{1}{2}{a^2}\\ \Rightarrow SB.AC.\cos \angle \left( {\overrightarrow {SB} ;\overrightarrow {AC} } \right) = - \frac{1}{2}{a^2}\\ \Leftrightarrow a.a.\cos \angle \left( {\overrightarrow {SB} ;\overrightarrow {AC} } \right) = - \frac{1}{2}{a^2}\\ \Leftrightarrow \cos \angle \left( {\overrightarrow {SB} ;\overrightarrow {AC} } \right) = - \frac{1}{2}\\ \Leftrightarrow \angle \left( {\overrightarrow {SB} ;\overrightarrow {AC} } \right) = {120^0}\end{array}\).
Chọn D.