Câu hỏi
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên.
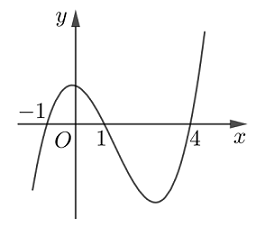
Hàm số \(y = f\left( {{x^2} - 1} \right)\) có bao nhiêu điểm cực trị?
- A \(5\).
- B \(7\).
- C \(4\).
- D \(3\).
Phương pháp giải:
- Đặt \(y = g\left( x \right) = f\left( {{x^2} - 1} \right)\).
- Tính đạo hàm hàm số \(y = g\left( x \right)\) (đạo hàm hàm hợp).
- Giải phương trình \(g'\left( x \right) = 0\).
- Lập BBT và kết luận số điểm cực trị của hàm số.
Lời giải chi tiết:
Đặt \(y = g\left( x \right) = f\left( {{x^2} - 1} \right)\).
Ta có : \(g'\left( x \right) = \left( {{x^2} - 1} \right)'.f'\left( {{x^2} - 1} \right) = 2x.f'\left( {{x^2} - 1} \right)\)
Cho \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} - 1} \right) = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 1 = - 1\\{x^2} - 1 = 1\\{x^2} - 1 = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \\x = \pm \sqrt 5 \end{array} \right.\)
(Tất cả các nghiệm trên đều là nghiệm bội lẻ).
Bảng xét dấu \(g'\left( x \right)\):
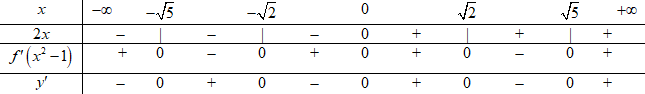
Vậy, hàm số \(y = f\left( {{x^2} - 1} \right)\) có tất cả 5 cực trị.
Chọn A.







