Câu hỏi
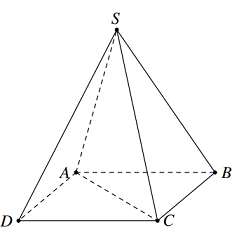
Cho hình chóp tứ giác đều \(S.ABCD\) có \(SA = a\sqrt {11} ,\) côsin góc tạo bởi hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) bằng \(\dfrac{1}{{10}}\). Thể tích của khối chóp \(S.ABCD\) bằng:
- A \(3{a^3}\)
- B \(12{a^3}\)
- C \(4{a^3}\)
- D \(9{a^3}\)
Phương pháp giải:
- Hình chóp tứ giác đều có các cạnh bên bằng nhau, các cạnh đáy bằng nhau và hình chiếu vuông góc của
đỉnh xuống mặt đáy trùng với tâm của đáy.
- Tìm góc tạo bởi giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) để tính cạnh đáy và chiều cao của khối chóp.
- Thể tích của khối chóp có chiều cao bằng \(h,\) diện tích đáy bằng \(S\) là \(V = \dfrac{1}{3}Sh\).
Lời giải chi tiết:
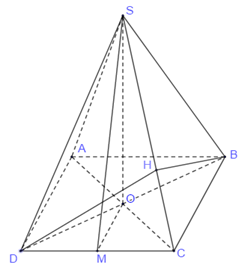
Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Do \(S.ABCD\) là hình chóp tứ giác đều nên \(ABCD\) là hình vuông, \(O\) là tâm của đáy nên \(SO \bot \left( {ABCD} \right)\).
Trong mp \(\left( {SCD} \right)\), kẻ \(DH \bot SC\,\,\,\left( {H \in SC} \right)\,\,\,\,\,\left( 1 \right)\), ta có:
\(ABCD\) là hình vuông nên \(AC \bot BD\)
\(\left\{ \begin{array}{l}AC \bot BD\\SO \bot \left( {ABCD} \right) \Rightarrow SO \bot BD\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\,\,\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(SC \bot \left( {DBH} \right) \Rightarrow SC \bot BH\)
Do đó, góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) là góc giữa 2 đường thẳng \(DH\) và \(BH\).
Lại có hai tam giác \(SBC\) và \(SCD\) là 2 tam giác cân bằng nhau. Suy ra\(DH = BH\)
Gọi độ dài cạnh của hình vuông \(ABCD\) là \(x\,\,\,\left( {x > 0} \right)\). Suy ra \(BD = AC = \sqrt 2 x\)
Gọi \(M\) là trung điểm \(DC\) thì \(DM = MC = \dfrac{x}{2}\)
Tam giác \(SCD\) cân tại \(S\) nên \(SM \bot CD\)
Theo định lí Pi – ta – go ta có: \(SM = \sqrt {S{D^2} - D{M^2}} = \sqrt {11{a^2} - \dfrac{{{x^2}}}{4}} \)
Do đó, \({S_{\Delta SCD}} = \dfrac{1}{2}SM.CD = \dfrac{1}{2}x.\sqrt {11{a^2} - \dfrac{{{x^2}}}{4}} \)
Suy ra \(BH = DH = \dfrac{{2{S_{\Delta SCD}}}}{{SC}} = \dfrac{{x.\sqrt {11{a^2} - \dfrac{{{x^2}}}{4}} }}{{\sqrt {11} a}} = x.\sqrt {1 - \dfrac{{{x^2}}}{{44{a^2}}}} \)
Theo giả thiết ta có: \(\cos \left( {\left( {SBC} \right);\left( {SCD} \right)} \right) = \dfrac{1}{{10}} \Rightarrow \cos BHD = \pm \dfrac{1}{{10}}\)
Ta có:
\(\begin{array}{l}\cos DHB = \dfrac{{D{H^2} + B{H^2} - B{D^2}}}{{2DH.BH}} = \dfrac{{2.{x^2}.\left( {1 - \dfrac{{{x^2}}}{{44{a^2}}}} \right) - 2{x^2}}}{{2{x^2}\left( {1 - \dfrac{{{x^2}}}{{44{a^2}}}} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{2{x^2}.\dfrac{{ - {x^2}}}{{44{a^2}}}}}{{\dfrac{{2{x^2}\left( {44{a^2} - {x^2}} \right)}}{{44{a^2}}}}} = \dfrac{{ - {x^2}}}{{44{a^2} - {x^2}}}\\ \Rightarrow \left[ \begin{array}{l}\dfrac{{{x^2}}}{{{x^2} - 44{a^2}}} = \dfrac{1}{{10}}\\\dfrac{{{x^2}}}{{{x^2} - 44{a^2}}} = - \dfrac{1}{{10}}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} = - \dfrac{{44}}{9}{a^2}\\{x^2} = 4{a^2}\end{array} \right. \Leftrightarrow x = 2a\end{array}\)
Suy ra \(SO = \sqrt {S{A^2} - A{O^2}} = \sqrt {11{a^2} - {{\left( {\sqrt 2 a} \right)}^2}} = 3a.\)
Thể tích của khối chóp đã cho là:\({S_{ABCD}} = \dfrac{1}{3}.SO.A{B^2} = \dfrac{1}{3}.3a.{\left( {2a} \right)^2} = 4{a^3}.\)
Chọn C.







