Câu hỏi
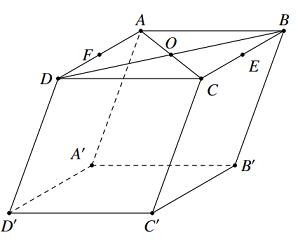
Cho hình hộp \(ABCD.A'B'C'D'\) có đáy \(ABCD\) là hình bình hành tâm \(O\) và \(AD = 2AB = 2a;\)\(\cos AOB = \dfrac{3}{5}\). Gọi \(E,\,\,F\) lần lượt là trung điểm của \(BC\) và \(AD\). Biết rằng \(CD' \bot CF;\,\,BB' \bot ED\) và khoảng cách giữa hai đường thẳng \(CD\) và \(AA'\) là \(a\sqrt 3 \), tính thể tích khối hộp \(ABCD.A'B'C'D'\).
- A \(\dfrac{{3{a^3}\sqrt 3 }}{2}\)
- B \(\dfrac{{{a^3}\sqrt 3 }}{3}\)
- C \(3{a^3}\sqrt 3 \)
- D \({a^3}\sqrt 3 \)
Phương pháp giải:
Sử dụng công thức đường trung tuyến và định lí hàm \(\cos \) để tính độ dài \(OA,\,\,OB\).
Dựa vào \(CD' \bot CF,\,\,\,BB' \bot ED;\,\,\,{d_{\left( {CD,AA'} \right)}} = a\sqrt 3 \) để tính chiều cao của khối hộp.
Thể tích của khối hộp có chiều cao \(h\) và diện tích đáy bằng \(S\) là \(V = Sh\)
Lời giải chi tiết:
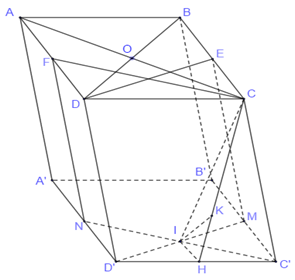
Vì \(ABCD\) là hình bình hành nên \(O\) là trung điểm của \(AC\) và \(BD\).
Theo công thức đường trung tuyến ta có:\(BO\) là trung tuyến trong tam giác \(ABC\) nên
\(B{O^2} = \dfrac{{B{A^2} + B{C^2}}}{2} - \dfrac{{A{C^2}}}{4}\)\( \Leftrightarrow O{B^2} = \dfrac{{{a^2} + 4{a^2}}}{2} - O{A^2}\)\( \Leftrightarrow O{A^2} + O{B^2} = \dfrac{{5{a^2}}}{2}\,\,\,\,\,\left( 1 \right)\)
Theo định lí hàm số cos ta có:
\(\begin{array}{l}\cos \angle AOB = \dfrac{{O{A^2} + O{B^2} - A{B^2}}}{{2OA.OB}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\dfrac{{5{a^2}}}{2} - {a^2}}}{{2OA.OB}} = \dfrac{{3{a^2}}}{{4OA.OB}}\\\cos \angle AOB = \dfrac{3}{5} \Rightarrow OA.OB = \dfrac{5}{4}{a^2}\,\,\,\,\left( 2 \right)\end{array}\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có: \(O{A^2} + O{B^2} - 2OA.OB = 0\)\( \Leftrightarrow {\left( {OA - OB} \right)^2} = 0 \Leftrightarrow OA = OB = \dfrac{{\sqrt 5 a}}{2}\)
Suy ra \(AC = DB\) mà \(ABCD\) là hình bình hành nên \(ABCD\) là hình chữ nhật.
Do \(AD = 2AB\) nên \(CDFE\) là hình vuông.
Gọi \(M,\,\,N\) lần lượt là trung điểm của \(B'C'\) và \(A'D'\), ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}CD' \bot CF\\MD'//ED \Rightarrow MD' \bot CF\end{array} \right. \Rightarrow CF \bot \left( {CMD'} \right)\,\,\,\,\,\,\left( 3 \right)\\\left\{ \begin{array}{l}DE \bot CF\\BB' \bot ED \Rightarrow CC' \bot ED\end{array} \right. \Rightarrow ED \bot \left( {CC'NF} \right)\,\,\,\,\,\left( 4 \right)\end{array}\)
Gọi \(I\) là giao điểm của \(C'N\) và \(D'M\). Từ (3) và (4) suy ra \(\left\{ \begin{array}{l}DE \bot CI\\CF \bot CI\end{array} \right. \Rightarrow CI \bot \left( {ABCD} \right)\)
Ta có:
\(\begin{array}{l}d\left( {CD;AA'} \right) = d\left( {\left( {CDD'C'} \right);\left( {ABB'A'} \right)} \right) = d\left( {B';\left( {CDD'C'} \right)} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2d\left( {M;\left( {CDD'C'} \right)} \right) = 4d\left( {I;\left( {CDD'C'} \right)} \right)\\ \Rightarrow d\left( {I;\left( {CDD'C'} \right)} \right) = \dfrac{{\sqrt 3 a}}{4}\end{array}\)
Gọi \(H\) là trung điểm của \(C'D'\). Khi đó, \(\left\{ \begin{array}{l}C'D' \bot IH\\C'D' \bot CI\end{array} \right. \Rightarrow C'D' \bot \left( {CIH} \right)\)\( \Rightarrow \left( {CDD'C'} \right) \bot \left( {CIH} \right)\,\,\,\,\,\,\left( 5 \right)\)
Trong mp \(\left( {CIH} \right)\), kẻ \(IK \bot CH\left( {K \in CH} \right)\). Suy ra \(\left( 5 \right) \Leftrightarrow IK \bot \left( {CDD'C'} \right) \Rightarrow IK = \dfrac{{\sqrt 3 a}}{4}\).
Tam giác \(CIH\) vuông tại \(I\) có đường cao \(IK\) nên
\(\dfrac{1}{{I{K^2}}} = \dfrac{1}{{I{C^2}}} + \dfrac{1}{{I{H^2}}}\)\( \Leftrightarrow \dfrac{1}{{{{\left( {\dfrac{{\sqrt 3 }}{4}a} \right)}^2}}} = \dfrac{1}{{I{C^2}}} + \dfrac{1}{{{{\left( {\dfrac{a}{2}} \right)}^2}}}\)\( \Rightarrow IC = \dfrac{{\sqrt 3 a}}{2}\)
Do \(CI \bot \left( {ABCD} \right)\) nên thể tích của hình hộp \(ABCD.A'B'C'D'\) là:
\({V_{ABCD.A'B'C'D'}} = CI.{S_{ABCD}} = CI.AB.AD = \dfrac{{\sqrt 3 }}{2}a.a.2a = \sqrt 3 {a^3}.\)
Chọn D.







