Câu hỏi
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(B\) với \(AB = a,\) \(AA' = 2a,\)\(A'C = 3a\). Gọi \(M\) là trung điểm của \(A'C'\), \(I\) là giao điểm của đường thẳng \(AM\) và \(A'C\). Tính theo \(a\) thể tích khối \(IABC\).
- A \(V = \dfrac{2}{3}{a^3}\)
- B \(V = \dfrac{2}{9}{a^3}\)
- C \(V = \dfrac{4}{9}{a^3}\)
- D \(V = \dfrac{4}{3}{a^3}\)
Phương pháp giải:
+) So sánh thể tích của khối tứ diện \(IABC\) với thể tích của khối lăng trụ.
+) Tính thể tích khối lăng trụ.
Lời giải chi tiết:
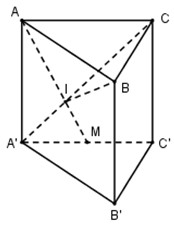
Ta có: \(A'M\parallel AC \Rightarrow \dfrac{{A'M}}{{AC}} = \dfrac{{A'I}}{{IC}} = \dfrac{1}{2} \Rightarrow \dfrac{{IC}}{{A'C}} = \dfrac{2}{3}.\)
Vì \(IA' \cap \left( {ABC} \right) = C\)\( \Rightarrow \dfrac{{d\left( {I;\left( {ABC} \right)} \right)}}{{d\left( {A';\left( {ABC} \right)} \right)}} = \dfrac{{IC}}{{A'C}} = \dfrac{2}{3}.\)
\(\begin{array}{l} \Rightarrow \dfrac{{{V_{I.ABC}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}d\left( {I;\left( {ABC} \right)} \right).{S_{ABC}}}}{{d\left( {A';\left( {ABC} \right)} \right).{S_{ABC}}}} = \dfrac{1}{3}.\dfrac{2}{3} = \dfrac{2}{9}\\ \Rightarrow {V_{I.ABC}} = \dfrac{2}{9}{V_{ABC.A'B'C'}}\end{array}\)
Ta có: \(AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot AC \Rightarrow \Delta AA'C\) vuông tại \(A\).
\( \Rightarrow AC = \sqrt {A'{C^2} - AA{'^2}} = \sqrt {9{a^2} - 4{a^2}} = a\sqrt 5 .\)
Xét tam giác vuông ABC có: \(BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {5{a^2} - {a^2}} = 2a.\)
\( \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}a.2a = {a^2}.\)
\( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = 2a.{a^2} = 2{a^3}.\)
Vậy \({V_{I.ABC}} = \dfrac{2}{9}{V_{ABC.A'B'C'}} = \dfrac{2}{9}.2{a^3} = \dfrac{{4{a^3}}}{9}.\)
Chọn C.







