Câu hỏi
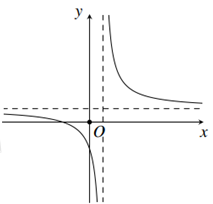
Cho hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\)\(\left( {d < 0} \right)\) có đồ thị như hình bên. Khẳng định nào dưới đây là đúng?
- A \(a < 0,\,\,b > 0,\,\,c < 0\)
- B \(a > 0,\,\,b > 0,\,\,c > 0\)
- C \(a > 0,\,\,b > 0,\,\,c < 0\)
- D \(a > 0,\,\,b < 0,\,\,c > 0\)
Phương pháp giải:
- Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) \(\left( {ad - bc \ne 0} \right)\) nhận đường thẳng \(y = \dfrac{a}{c}\) là tiệm cận ngang và \(x = \dfrac{{ - d}}{c}\) là tiệm cận đứng.
- Đồ thị này cắt trục hoành tại điểm có hoành độ \(x = - \dfrac{b}{a}\) và cắt trục tung tại điểm có tung độ bằng \(y = \dfrac{b}{d}\).
Lời giải chi tiết:
Từ đồ thị hàm số đã cho ta thấy :
+) Hàm số có 1 đường tiệm cận đứng là \(x = m > 0\) nên \(\dfrac{{ - d}}{c} > 0 \Leftrightarrow \dfrac{d}{c} < 0,\,\,\,d < 0 \Rightarrow c > 0\).
+) Hàm số có 1 đường tiệm cận ngang là \(y = n > 0\) nên \(\dfrac{a}{c} > 0,\,\,\,c > 0 \Rightarrow a > 0\).
+) Đồ thị hàm số cắt trục tung tại điểm có tung độ âm nên \(\dfrac{b}{d} < 0,\,\,\,d < 0 \Rightarrow b > 0\).
Vậy \(a > 0,\,\,b > 0,\,\,c > 0\).
Chọn B.







