Câu hỏi
Đường cong trong hình vẽ bên là của hàm số nào trong 4 hàm số dưới đây?
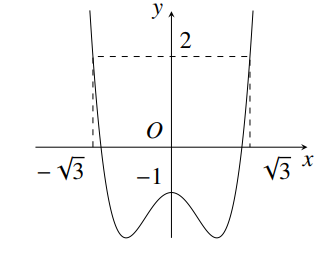
- A \(y = - {x^4} + 2{x^2} - 1\)
- B \(y = - {x^3} + 3{x^2} - 1\)
- C \(y = {x^4} - {x^2} - 4\)
- D \(y = {x^4} - 2{x^2} - 1\)
Phương pháp giải:
Tìm các giới hạn \(\mathop {\lim }\limits_{x \to \pm \infty } y\), số điểm cực trị, điểm cắt của đồ thị với trục tung, các điểm được cho trong đồ thị để xác định hàm số của đồ thị đã cho.
Lời giải chi tiết:
Từ đồ thị hàm số đã cho ta thấy:
+) Hàm số đã cho có 3 điểm cực trị nên hàm số là hàm bậc 4, không thể là hàm bậc 3.
+) Hàm số nhận đường thẳng \(x = 0\) là trục đối xứng nên là hàm bậc 4 trùng phương, có dạng \(y = a{x^4} + b{x^2} + c\).
+) \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \) nên \(a > 0.\)
+) Hàm số cắt trục tung tại điểm có tung độ bằng \( - 1\) nên \(c = - 1.\)
Do đó, hàm số có đồ thị như hình vẽ là \(y = {x^4} - 2{x^2} - 1\).
Chọn D.







