Phương pháp giải:

- Sử dụng công thức \({V_{M.A'BN}} = \dfrac{1}{3}.d\left( {M;\left( {A'BN} \right)} \right).{S_{A'BN}}\) để tính khoảng cách từ \(M\) đến \(\left( {A'BN} \right)\).

- Tính thể tích khối chóp \(M.A'BN\) (coi đỉnh là \(N\)) dựa vào thể tích lăng trụ.

- Tính các cạnh của tam giác \(A'BN\) nhờ định lí Pytago.

- Sử dụng công thức He-rong để tính diện tích tam giác: \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) trong đó \(p\) là nửa chu vi, \(a,\,\,b,\,\,c\) là độ dài 3 cạnh của tam giác.

Lời giải chi tiết:

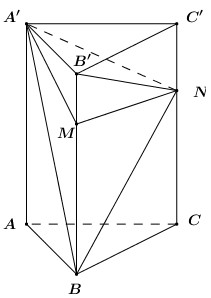
Ta có: \(\left\{ \begin{array}{l}AB = 1\\AC = 2\\\angle BAC = {120^0}\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{S_{ABC}} = \dfrac{1}{2}.AB.AC.\sin A = \dfrac{{\sqrt 3 }}{2}\\BC = \sqrt {A{C^2} + A{B^2} - 2AB.AC.\cos A}  = \sqrt 7 \end{array} \right.\).

Lại có: \(\dfrac{{{S_{A'BM}}}}{{{S_{A'BB'}}}} = \dfrac{{BM}}{{BB'}} = \dfrac{3}{4} \Rightarrow \dfrac{{{V_{N.A'BM}}}}{{{V_{N.A'BB'}}}} = \dfrac{3}{4}\).

Mà \({V_{N.A'BB'}} = {V_{C'.A'BB'}} = {V_{B.A'B'C'}} = \dfrac{1}{3}.{V_{ABC.A'B'C'}}\).

\( \Rightarrow {V_{N.A'BM}} = \dfrac{1}{4}{V_{ABC.A'B'C'}} = \dfrac{1}{4}.AA'.{S_{ABC}} = \dfrac{1}{4}.3.\dfrac{{\sqrt 3 }}{2} = \dfrac{{3\sqrt 3 }}{8}\).

Áp dụng định lí Pytago trong các tam giác vuông ta có:

\(\begin{array}{l}A'B = \sqrt {A'{A^2} + A{B^2}}  = \sqrt {{3^2} + {1^2}}  = \sqrt {10} \\BN = \sqrt {B{C^2} + C{N^2}}  = \sqrt {{{\left( {\sqrt 7 } \right)}^2} + {{\left( {\dfrac{2}{3}.3} \right)}^2}}  = \sqrt {11} \\A'N = \sqrt {A'C{'^2} + C'{N^2}}  = \sqrt {{2^2} + {{\left( {\dfrac{1}{3}.3} \right)}^2}}  = \sqrt 5 \end{array}\)

\( \Rightarrow \) Nửa chu vi tam giác \(A'BN\) là: \(p = \dfrac{{A'B + BN + A'N}}{2} = \dfrac{{\sqrt {10}  + \sqrt {11}  + \sqrt 5 }}{2}\)

Khi đó áp dụng công thức He-rong ta tính được: \({S_{A'BN}} = \sqrt {p\left( {p - A'B} \right)\left( {p - BN} \right)\left( {p - A'N} \right)}  = \dfrac{{\sqrt {46} }}{2}\).

Ta lại có: \({V_{M.A'BN}} = \dfrac{1}{3}.d\left( {M;\left( {A'BN} \right)} \right).{S_{A'BN}}\).

\( \Rightarrow d\left( {M;\left( {A'BN} \right)} \right) = \dfrac{{3{V_{M.A'BN}}}}{{{S_{A'BN}}}} = \dfrac{{3.\dfrac{{3\sqrt 3 }}{8}}}{{\dfrac{{\sqrt {46} }}{2}}} = \dfrac{{9\sqrt {138} }}{{184}}.\)

Chọn B.