Phương pháp giải:

- Xác định các điểm \(M,\,\,N\).

- Đặt \(\dfrac{{SM}}{{SB}} = x,\,\,\,\dfrac{{SN}}{{SD}} = y\), tính tỉ số thể tích \(\dfrac{{{V_1}}}{V}\) bằng 2 cách theo \(x,\,\,y\).

- Rút \(x\) theo \(y\) hoặc ngược lại, tỉ số thể tích \(\dfrac{{{V_1}}}{V}\) lúc này chỉ được tính theo 1 ẩn \(x\) hoặc \(y\), sử dụng phương pháp hàm số để tìm GTNN của hàm số.

Lời giải chi tiết:

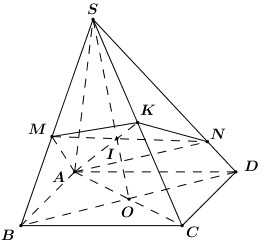
Gọi mặt phẳng chứa \(AK,\) cắt \(SB,\,\,SD\) lần lượt tại \(M,\,\,N\) là \(\left( \alpha  \right)\) .

Trong \(\left( {SAC} \right)\) gọi \(I = AC \cap SO\).

Trong \(\left( {SBD} \right)\), lấy \(M \in SB\), nối \(MI\) cắt \(SD\) tại \(N\).

Khi đó ta có \(\left( \alpha  \right) \equiv \left( {AMKN} \right)\).

Đặt: \(\dfrac{{SM}}{{SB}} = x,\,\,\,\dfrac{{SN}}{{SD}} = y.\)

Ta có:

\(\begin{array}{l}\dfrac{{{V_1}}}{V} = \dfrac{{{V_{SAMNK}}}}{{{V_{SABCD}}}} = \dfrac{1}{2}.\dfrac{{{V_{SAMK}} + {V_{SANK}}}}{{{V_{SABC}}}}\\\,\,\,\,\,\, = \dfrac{1}{2}.\left( {\dfrac{{SM}}{{SB}}.\dfrac{{SK}}{{SC}} + \dfrac{{SN}}{{SD}}.\dfrac{{SK}}{{SC}}} \right) = \dfrac{1}{4}\left( {x + y} \right)\end{array}\)

Lại có:  

\(\begin{array}{l}\dfrac{{{V_1}}}{V} = \dfrac{{{V_{S.AMKN}}}}{{{V_{S.ABCD}}}} = \dfrac{1}{2}.\dfrac{{{V_{SAMN}} + {V_{SKMN}}}}{{{V_{SABD}}}}\\\,\,\,\,\,\,\, = \dfrac{1}{2}\left( {\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}} + \dfrac{{SK}}{{SC}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}}} \right)\\\,\,\,\,\,\,\, = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SD}}.\left( {\dfrac{1}{2} + \dfrac{1}{2}.\dfrac{{SK}}{{SC}}} \right) = \dfrac{3}{4}xy\end{array}\)

Từ đó ta có: \( \Rightarrow \dfrac{3}{4}xy = \dfrac{1}{4}\left( {x + y} \right)\)\( \Rightarrow x + y = 3xy \Leftrightarrow x = y\left( {3x - 1} \right)\)\( \Rightarrow y = \dfrac{x}{{3x - 1}}\).

Do \(x,\,\,y > 0 \Rightarrow 3x - 1 > 0 \Leftrightarrow x > \dfrac{1}{3}\).

Khi đó ta có: \(\dfrac{{{V_1}}}{V} = \dfrac{3}{4}xy = \dfrac{3}{4}.\dfrac{{{x^2}}}{{3x - 1}}\) với \(x > \dfrac{1}{3}\).

Đặt \(f\left( x \right) = \dfrac{{{x^2}}}{{3x - 1}}\) ta có:

\(\begin{array}{l}f'\left( x \right) = \dfrac{{2x\left( {3x - 1} \right) - 3{x^2}}}{{{{\left( {3x - 1} \right)}^2}}} = \dfrac{{x\left( {3x - 2} \right)}}{{{{\left( {3x - 1} \right)}^2}}}\\f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\left( {ktm} \right)\\x = \dfrac{2}{3}\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)

Bảng biến thiên:

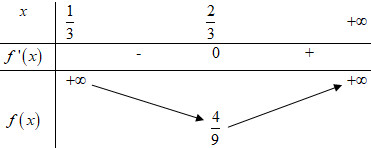
Dựa vào BBT ta thấy: \(\mathop {\min }\limits_{\left( {\dfrac{1}{3}; + \infty } \right)} f\left( x \right) = f\left( {\dfrac{2}{3}} \right) = \dfrac{4}{9}\).

Vậy giá trị nhỏ nhất của \(\dfrac{{{V_1}}}{V}\) là \(\dfrac{3}{4}.\dfrac{4}{9} = \dfrac{1}{3}\), đạt được khi \(\dfrac{{SM}}{{SB}} = \dfrac{{SN}}{{SD}} = \dfrac{2}{3}\).

Chọn D.