Phương pháp giải:

Sử dụng tính chất của tam giác đồng dạng

Lời giải chi tiết:

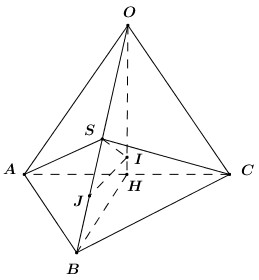
Tam giác \(OAB\) có \(\left\{ \begin{array}{l}OA = OB\,\,\left( {gt} \right)\\\angle AOB = {60^0}\,\,\left( {gt} \right)\end{array} \right. \Rightarrow \Delta OAB\) đều \( \Rightarrow AB = a\).

Tam giác \(OBC\) có \(\left\{ \begin{array}{l}OB = OC\,\,\left( {gt} \right)\\\angle BOC = {90^0}\,\,\left( {gt} \right)\end{array} \right. \Rightarrow \Delta OBC\) vuông cân tại \(O\) \( \Rightarrow BC = a\sqrt 2 \).

Tam giác \(OAC\) có \(\left\{ \begin{array}{l}OA = OC\,\,\left( {gt} \right)\\\angle AOC = {120^0}\end{array} \right.\), áp dụng định lí Cosin trong tam giác ta có

\(AC = \sqrt {O{A^2} + O{C^2} - 2OA.OC.\cos \angle AOC}  = a\sqrt 3 \).

Khi đó ta có \(A{C^2} = A{B^2} + A{C^2}\), do đó tam giác \(ABC\) vuông tại \(B\) (định lí Pytago đảo).

Gọi \(H\) là trung điểm của \(AC\), suy ra \(H\) là tâm đường tròn ngoại tiếp \(\Delta ABC\).

Chóp \(O.ABC\) có các cạnh bên bằng nhau, do đó chân đường cao trùng với tâm đường tròn ngoại tiếp đáy nên \(OH \bot \left( {ABC} \right)\), suy ra \(OH \bot HB\) \( \Rightarrow \Delta OBH\) vuông tại \(H\).

Gọi \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\), \(J\) là trung điểm của \(SB\).

Vì \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABC\) nên \(IS = IA = IB = IC\) \( \Rightarrow IS = IB\) và \(I \in OH\).

\( \Rightarrow \Delta ISB\) cân tại \(I\), do đường trùng tuyến \(IJ\) đồng thời là đường cao \( \Rightarrow IJ \bot SB\).

Xét \(\Delta OIJ\) và \(\Delta OBH\) có:

\(\angle BOH \) chung;

\(\angle SJI = \angle SHB = {90^0}\).

\( \Rightarrow \Delta OIJ \sim \Delta OBH\,\,\left( {g.g} \right)\)

\( \Rightarrow \dfrac{{OJ}}{{OH}} = \dfrac{{IJ}}{{HB}} \Rightarrow IJ = \dfrac{{OJ.HB}}{{OH}}\).

Ta có: \(OJ = \dfrac{3}{4}OB = \dfrac{3}{4}a\).

Tam giác \(ABC\) vuông tại \(B\) nên \(HB = \dfrac{1}{2}AC = \dfrac{{a\sqrt 3 }}{2}\).

Áp dụng định lí Pytago trong tam giác vuông  có: \(OH = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2}}  = \dfrac{a}{2}\).

\(\begin{array}{l} \Rightarrow IJ = \dfrac{{\dfrac{{3a}}{4}.\dfrac{{a\sqrt 3 }}{2}}}{{\dfrac{a}{2}}} = \dfrac{{3a\sqrt 3 }}{4}\\ \Rightarrow R = SI = \sqrt {S{J^2} + I{J^2}}  = \sqrt {{{\left( {\dfrac{a}{4}} \right)}^2} + {{\left( {\dfrac{{3a\sqrt 3 }}{4}} \right)}^2}}  = \dfrac{{a\sqrt 7 }}{2}.\end{array}\)

Chọn D.