Phương pháp giải:

- Chứng minh tứ giác \(AHEK\) nội tiếp đường tròn đường kính \(HK\).

- Xác định trục của tứ giác \(AHEK\), cắt đường trung trực của \(SH\) tại \(M\).

- Chứng minh \(M\) là tâm mặt cầu ngoại tiếp chóp \(S.AHEK\).

- Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông và định lí Pytago để tính bán kính mặt cầu.

- Thể tích khối cầu bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\).

Lời giải chi tiết:

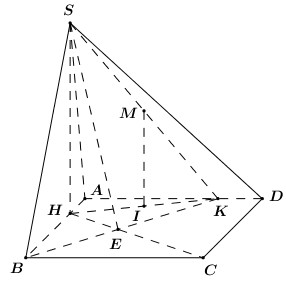
Xét \(\Delta HBC\) và \(\Delta KAB\) có:

\(\angle HBC = \angle KAB = {90^0}\);

\(HB = KA = 3a\);

\(BC = AB = 4a\).

\( \Rightarrow \Delta HBC = \Delta KAB\,\,\,\left( {c.g.c} \right)\) \( \Rightarrow \angle HCB = \angle KBA\) (hai góc tương ứng).

Mà \(\angle KBA + \angle KBC = {90^0}\) nên \(\angle KBC + \angle HCB = {90^0}\), do đó tam giác \(EBC\) vuông tại \(E\) hay \(BK \bot HC\).

Gọi \(I\) là trung điểm của \(HK\), ta có: \(\angle HAK = \angle HEK = {90^0}\), do đó \(AHEK\) là tứ giác nội tiếp đường tròn tâm \(I\) đường kính \(HK\).

Trong \(\left( {SHK} \right)\) kẻ đường thẳng song song với \(SH\) cắt \(SK\) tại \(M\), ta có:

\(\left\{ \begin{array}{l}SH \bot \left( {ABCD} \right)\\d\parallel SH\end{array} \right. \Rightarrow d \bot \left( {ABCD} \right) \Rightarrow d \bot \left( {AHEK} \right)\) tại \(I\), mà \(I\) là tâm đường tròn ngoại tiếp tứ giác \(AHEK\) nên \(MA = MH = ME = MK\,\,\,\left( 1 \right)\).

Xét tam giác \(SHK\) có: \(I\) là trung điểm của \(HK\).

                                   \(IM\parallel SH\) (theo cách dựng)

\( \Rightarrow M\) là trung điểm của \(SK\) (định lí đường trung bình của tam giác).

Mà \(SH \bot \left( {ABCD} \right)\) nên \(SH \bot HK\), suy ra tam giác \(SHK\) vuông tại \(H\), do đó \(M\) là tâm đường tròn ngoại tiếp tam giác \(SHK\) hay \(MS = MH = MK\,\,\,\left( 2 \right)\).

Từ (1) và (2) \( \Rightarrow MA = MH = ME = MK = MS\), suy ra \(M\) là tâm khối cầu ngoại tiếp \(S.AHEK\), bán kính khối cầu là \(R = \dfrac{{SK}}{2}.\)

Tam giác \(SHB\) vuông tại \(H\) có \(BH = 3a\), \(\angle SBH = {30^0}\,\,\left( {gt} \right)\) nên \(SH = HB.tan{30^0} = 3a.\dfrac{{\sqrt 3 }}{3} = a\sqrt 3 \).

Áp dụng định lí Pytago ta có:

\(\begin{array}{l}HK = \sqrt {A{H^2} + A{K^2}}  = \sqrt {{a^2} + {{\left( {3a} \right)}^2}}  = a\sqrt {10} \\SK = \sqrt {H{K^2} + S{H^2}}  = \sqrt {{{\left( {\sqrt 3 a} \right)}^2} + {{\left( {\sqrt {10} a} \right)}^2}}  = a\sqrt {13} \\ \Rightarrow R = \dfrac{{SK}}{2} = \dfrac{{a\sqrt {13} }}{2}\end{array}\)

Vậy thể tích khối cầu ngoại tiếp chóp \(S.AHEK\) là: \(V = \dfrac{4}{3}.\pi .{R^3} = \dfrac{4}{3}\pi {\left( {\frac{{a\sqrt {13} }}{2}} \right)^3} = \dfrac{{13\pi {a^3}\sqrt {13} }}{6}.\)

Chọn A.