Phương pháp giải:

Tam giác ABC vuông tại A suy ra A, B, C nằm trên mặt cầu đường kính BC.

Lời giải chi tiết:

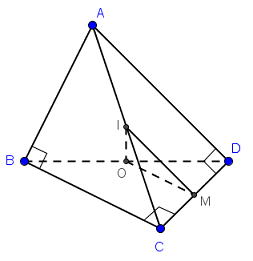
Gọi I, O, M lần lượt là trung điểm của AC, BD, CD.

Do \(\widehat {ABC} = \widehat {ADC} = {90^0}\) nên A, B, C, D nằm trên mặt cầu (S) tâm I, đường kính AC.

Lại có, tam giác BCD vuông tại C \( \Rightarrow \) O là tâm đường tròn (C) ngoại tiếp tam giác BCD (trên mặt phẳng (BCD)

\( \Rightarrow OI \bot \left( {BCD} \right)\)

Ta có: \(OM//BC,\,\,IM//CD,\,\) góc giữa hai đường thẳng \(BC\) và \(AD\) bằng \({60^0} \Rightarrow \left( {\widehat {IM;OM}} \right) = {60^0}\)

\( \Rightarrow \Delta OIM\) vuông tại O và \(\widehat {IMO} = {60^0}\).

Ta có: \(BD = \sqrt {B{C^2} + C{D^2}}  = \sqrt {{a^2} + {{\left( {a\sqrt 3 } \right)}^2}}  = 2a \Rightarrow r = a\) (bán kính đường tròn (C)

Khoảng cách từ tâm I đến (BCD): \(d = OI = OM.\tan \widehat {IMO} = \dfrac{1}{2}.a.\tan {60^0} = \dfrac{{a\sqrt 3 }}{2}\)

Ta có: \({R^2} = {r^2} + {d^2} = {a^2} + {\left( {\dfrac{{a\sqrt 3 }}{2}} \right)^2} = \dfrac{{7{{\rm{a}}^2}}}{4} \Leftrightarrow R = \dfrac{{a\sqrt 7 }}{2}\) (R là bán kính mặt cầu (S)).

Chọn D.