Câu hỏi
Trong không gian cho tam giác \(OIM\) vuông tại \(I\), góc \(\angle IOM = {45^0}\)và cạnh \(IM = a\). Khi quay tam giác \(OIM\) quanh cạnh \(OI\) thì đường gấp khúc \(OIM\)tạo thành một hình nón tròn xoay. Diện tích xung quanh của hình nón tròn xoay đó bằng:
- A \(\pi {a^2}\sqrt 2 \)
- B \(\pi {a^2}\sqrt 3 \)
- C \(\dfrac{{\pi {a^2}\sqrt 2 }}{2}\)
- D \(\pi {a^2}\)
Phương pháp giải:
Sử dụng công thức tính diện tích xung quanh của hình nón bán kính đáy đáy \(r\), đường sinh \(l\) là \({S_{xq}} = \pi rl\).
Lời giải chi tiết:
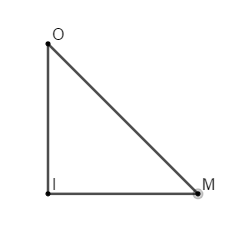
Khi quay tam giác vuông \(OIM\) xung quanh cạnh \(OI\) ta được hình nón có bán kính đáy \(r = IM\), đường sinh \(l = OM\).
Tam giác \(OIM\) vuông tại \(I\) có góc \(\angle IOM = {45^0}\)nên là tam giác vuông cân \( \Rightarrow IM = IO = a,\,\,OM = a\sqrt 2 .\)
Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi .IM.OM = \pi {a^2}\sqrt 2 .\)
Chọn A.







