Phương pháp giải:

- Chia thể tích khối tròn xoay ra thành những phần nhỏ rồi cộng vào.

- Thể tích khối nón có chiều cao \(h\), bán kính đáy \(r\) là \(V = \dfrac{1}{3}\pi {r^2}h\).

- Thể tích khối nón cụt có chiều cao \(h\), hai bán kính đáy \({r_1},\,\,{r_2}\) là: \(V = \dfrac{h}{3}\left( {r_1^2 + {r_1}{r_2} + r_2^2} \right)\).

Lời giải chi tiết:

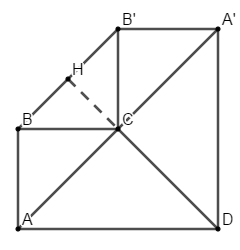
Lấy điểm \(A',\,\,B'\)  lần lượt là điểm đối xứng với \(A,\,\,B\) qua \(CD\).

Gọi \(H,\,\,C\) là trung điểm của \(BB',\,\,AA'\) .

Ta có các tam giác \(ABC,\,\,HBC\) là các tam giác vuông cân tại \(B,\,\,H\).

\(\begin{array}{l}AC = \sqrt {B{C^2} + A{B^2}}  = a\sqrt 2  = CD\\BH = \dfrac{{BC}}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }} = CH\end{array}\)

Gọi \({V_1}\)  là thể tích khối nón chiều cao \(CD\), đường kính đáy \(AA'\).

\( \Rightarrow {V_1} = \dfrac{1}{3}.\pi A{C^2}.CD = \dfrac{1}{3}\pi {\left( {a\sqrt 2 } \right)^2}.a\sqrt 2  = \dfrac{{2\sqrt 2 \pi {a^3}}}{3}\)

Gọi \({V_2}\) là thể tích khối nón cụt có chiều cao \(CH\), đáy nhỏ bán kính \(BH\), đáy lớn bán kính \(AC\).

\(\begin{array}{l} \Rightarrow {V_2} = \dfrac{{\pi .CH}}{3}.\left( {A{C^2} + B{H^2} + AC.BH} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\pi \dfrac{a}{{\sqrt 2 }}}}{3}.\left( {{{\left( {a\sqrt 2 } \right)}^2} + {{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2} + \dfrac{a}{{\sqrt 2 }}.a\sqrt 2 } \right) = \dfrac{{7\sqrt 2 \pi {a^3}}}{{12}}\end{array}\)

Gọi \({V_3}\)là thể tích khối nón chiều cao \(CH\), bán kính đáy \(BH\).

\( \Rightarrow {V_3} = \dfrac{1}{3}\pi B{H^2}.CH = \dfrac{1}{3}\pi {\left( {\dfrac{a}{{\sqrt 2 }}} \right)^2}.\dfrac{a}{{\sqrt 2 }} = \dfrac{{\sqrt 2 \pi {a^3}}}{{12}}\)

Vậy \(V = {V_1} + {V_2} - {V_3} = \dfrac{{2\sqrt 2 \pi {a^3}}}{3} + \dfrac{{7\sqrt 2 \pi {a^3}}}{{12}} - \dfrac{{\sqrt 2 \pi {a^3}}}{{12}} = \dfrac{{7\sqrt 2 \pi {a^3}}}{6}.\)

Chọn D.