Câu hỏi
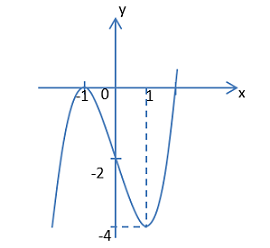
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ. Tìm \(m\) để phương trình \(f\left( {\sin x} \right) = m\) có nghiệm \(x \in \left( {0;\pi } \right)\).
- A \(m \in \left[ { - 4; - 2} \right]\)
- B \(m \in \left( { - 4; - 2} \right)\)
- C \(m \in \left[ { - 4; - 2} \right)\)
- D \(m \in \left[ { - 4;0} \right]\backslash \left\{ { - 2} \right\}\)
Lời giải chi tiết:
Với xÎ(0;p) thì \(\sin \,x \in \left( {0;1} \right]\). Xét hàm số \(f\left( x \right)\) trên nửa khoảng \(\left( {0;1} \right]\), ta có:
Tập giá trị của \(f\left( x \right)\) trên nửa khoảng \(\left( {0;1} \right]\) là: \(\left[ { - 4; - 2} \right)\).
Do đó, để phương trình f(sinx)=m có nghiệm xÎ(0;p) thì m Î [-4;-2).
Chọn C.
Câu hỏi trước
