Câu hỏi
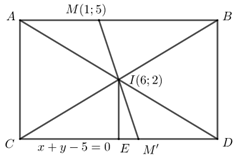
Trong mặt phẳng tọa độ \(Oxy\), cho hình chữ nhật \(ABCD\) với \(I\left( {6;\,\,2} \right)\) là giao điểm của hai đường chéo \(M\left( {1;\,\,5} \right)\) thuộc đoạn thẳng \(AB\), đường thẳng \(CD\) có phương trình \(x + y - 5 = 0\). Tọa độ trung điểm \(E\) của \(CD\) là:
- A \(E\left( {6;\,\, - 1} \right)\) và \(E\left( {7;\,\, - 2} \right)\)
- B \(E\left( {6;\,\,1} \right)\) và \(E\left( {7;\,\,2} \right)\)
- C \(E\left( { - 6;\,\, - 1} \right)\) và \(E\left( { - 7;\,\, - 2} \right)\)
- D \(E\left( { - 1;\,\,6} \right)\) và \(E\left( {2;\,\, - 7} \right)\)
Phương pháp giải:
+ Lấy điểm \(M'\) đối xứng với \(M\) qua \(I.\) Xác định tọa độ điểm \(M'\).
+ \(IE \bot EM'\). Để xác định điểm \(E\) từ CT \(\overrightarrow {IE} \,.\,\overrightarrow {EM'} = 0\).
Lời giải chi tiết:
Gọi \(M'\left( {{x_{M'}};\,\,{y_{M'}}} \right)\) là điểm đối xứng với \(M\left( {1;\,\,5} \right)\) qua \(I\left( {6;\,\,2} \right)\)\( \Rightarrow I\)là trung điểm của \(MM'.\)
Ta có: \(\left\{ \begin{array}{l}6 = \frac{{1 + {x_{M'}}}}{2}\\2 = \frac{{5 + {y_{M'}}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 + {x_{M'}} = 12\\5 + {y_{M'}} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{M'}} = 11\\{y_{M'}} = - 1\end{array} \right. \Rightarrow M'\left( {11;\,\, - 1} \right)\)
Vì \(E \in \left( {CD} \right):\,\,x + y - 5 = 0 \Rightarrow E\left( {t;\,\,5 - t} \right)\)
Ta có:
+)\(E\left( {t;\,\,5 - t} \right)\); \(I\left( {6;\,\,2} \right)\)\( \Rightarrow \overrightarrow {IE} = \left( {t - 6;\,\,3 - t} \right)\)
+) \(E\left( {t;\,\,5 - t} \right);\,\,M'\left( {11;\,\, - 1} \right) \Rightarrow \overrightarrow {EM'} = \left( {11 - t;\,\, - 6 + t} \right)\)
\(ABCD\) là hình chữ nhật, \(I\) là giao điểm hai đường chéo, \(E\) là trung điểm của \(CD\)\( \Rightarrow IE \bot CD\)\( \Rightarrow IE \bot EM'\)
\( \Rightarrow \overrightarrow {IE} \,.\,\,\overrightarrow {EM'} = 0\)
\( \Rightarrow \left( {t - 6} \right).\left( {11 - t} \right) + \left( {3 - t} \right).\left( { - 6 + t} \right) = 0\)
\( \Leftrightarrow 11t - {t^2} + 6t - 66 - 18 + 3t + 6t - {t^2} = 0\)
\( \Leftrightarrow - 2{t^2} + 26t - 84 = 0\)\( \Leftrightarrow {t^2} - 13t - 42 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 6\\t = 7\end{array} \right.\)\( \Rightarrow E\left( {6;\,\, - 1} \right)\) và \(E\left( {7;\,\, - 2} \right)\)
Chọn A