Câu hỏi
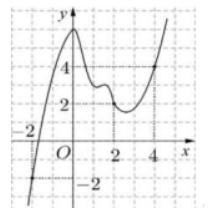
Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e\,\,\left( {a \ne 0} \right)\) và \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Đồ thị hàm số \(g\left( x \right) = \left| {2f\left( x \right) - {x^2}} \right|\) có tối đa bao nhiêu điểm cực trị?
- A \(7.\)
- B \(5.\)
- C \(6.\)
- D \(3.\)
Lời giải chi tiết:
\(\begin{array}{l}y = f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e\,\,\left( {a \ne 0} \right)\\ \Rightarrow f'\left( x \right) = 4{\rm{a}}{x^3} + 3b{x^2} + 2cx + d\end{array}\)
Đồ thị hàm số \(y = f'\left( x \right)\) đi qua các điểm \(\left( { - 2; - 2} \right),\,\left( {0;6} \right),\,\left( {2;2} \right),\,\left( {4;4} \right)\)
\( \Rightarrow \left\{ \begin{array}{l} - 32{\rm{a}} + 12b - 4c + d = - 2\\d = 6\\{\rm{32a}} + 12b + 4c + d = 2\\{\rm{256a}} + 48b + 8c + d = 4\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l} - 32{\rm{a}} + 12b - 4c = - 8\\{\rm{32a}} + 12b + 4c = - 4\\{\rm{256a}} + 48b + 8c = - 2\\d = 6\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{\rm{32a}} + 4c = 2\\b = - \dfrac{1}{2}\\{\rm{128a}} + 4c = 11\\d = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\rm{a}} = \dfrac{3}{{32}}\\b = - \dfrac{1}{2}\\c = - \dfrac{1}{4}\\d = 6\end{array} \right.\)
\(\begin{array}{l}g\left( x \right) = \left| {2f\left( x \right) - {x^2}} \right|\\\,\,\,\,\,\,\,\,\,\,\,\, = \left| {2\left( {\dfrac{3}{{32}}{x^4} - \dfrac{1}{2}{x^3} - \dfrac{1}{4}{x^2} + 6x + e} \right) - {x^2}} \right|\\\,\,\,\,\,\,\,\,\,\,\,\, = \left| {\dfrac{3}{{16}}{x^4} - {x^3} - \dfrac{3}{2}{x^2} + 12x + 2{\rm{e}}} \right|\end{array}\)
Xét hàm số \(h\left( x \right) = \dfrac{3}{{16}}{x^4} - {x^3} - \dfrac{3}{2}{x^2} + 12x + 2{\rm{e}}\)\( \Rightarrow h'\left( x \right) = \dfrac{3}{4}{x^3} - 3{x^2} - 3x + 12\).
\(h'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 2\\x = 4\end{array} \right.\)
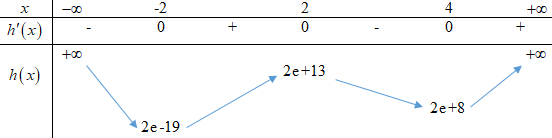
Đồ thị hàm số \(g\left( x \right) = \left| {2f\left( x \right) - {x^2}} \right|\) có tối đa 7 điểm cực trị (xảy ra khi và chỉ khi: \(2e + 8 < 0 < 2e + 13\)\( \Leftrightarrow - 6,5 < e < - 4\)).
Chọn A.







