Câu hỏi
Gọi \(m,\,\,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = \dfrac{1}{2}x - \sqrt {x + 2} \) trên đoạn \(\left[ { - 1;34} \right]\). Tính tổng \(S = 3m + M.\)
- A \(S = \dfrac{{13}}{2}\)
- B \(S = \dfrac{{63}}{2}\)
- C \(S = \dfrac{{25}}{2}\)
- D \(S = \dfrac{{11}}{2}\)
Phương pháp giải:
Tìm đạo hàm của hàm số.
Lập bảng biến thiên rồi kết luận.
Lời giải chi tiết:
TXĐ: \(D = \left[ {2; + \infty } \right)\).
Ta có \(y' = \dfrac{1}{2} - \dfrac{1}{{2\sqrt {x + 2} }}\)
\(y' = 0 \Leftrightarrow \sqrt {x + 2} = 1 \Leftrightarrow x + 2 = 1 \Leftrightarrow x = - 1\).
Bảng biến thiên:
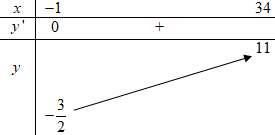
Dựa vào bảng biến thiên ta có \(m = - \dfrac{3}{2};M = 11.\)
Vậy \(S = 3m + M = \dfrac{{13}}{2}.\)
Chọn A.







