Phương pháp giải:

- Đặt ẩn phụ\(t = {2^x}\) \(\left( {t \in \left[ {a;b} \right]} \right)\), đưa về hàm chứa ẩn \(t\).

- Cô lập \(m\), đưa bất phương trình về dạng \(m < f\left( t \right)\,\,\,\forall t \in \left[ {a;b} \right]\)\( \Leftrightarrow m < \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( t \right)\).

- Lập BBT của hàm số \(y = f\left( t \right)\) và kết luận.

Lời giải chi tiết:

Đặt\(t = {2^x}\), với \(x \in \left[ {0;1} \right] \Rightarrow t \in \left[ {1;2} \right]\).

Khi đó bất phương trình trở thành  

\(\begin{array}{l}{t^2} - mt + 1 > 0\,\,\,\forall t \in \left[ {1;2} \right]\\ \Leftrightarrow \dfrac{{{t^2} + 1}}{t} > m\,\,\,\forall t \in \left[ {1;2} \right]\,\,\,\,\,\left( * \right)\end{array}\)

Đặt \(f\left( t \right) = \dfrac{{{t^2} + 1}}{t}\) ta có \(f'\left( t \right) = \dfrac{{{t^2} - 1}}{{{t^2}}} = 0 \Leftrightarrow t =  \pm 1\).

Bảng biến thiên:

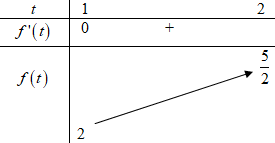
Dựa vào bảng biến thiên ta thấy (*) xảy ra khi \(m < \mathop {\min }\limits_{\left[ {1;2} \right]} f\left( t \right) \Leftrightarrow m < 2\).

Chọn B.