Phương pháp giải:

- Xét dấu biểu thức \(\dfrac{{{x^2} - x - 2}}{{x - 1}}\) sau đó chia các khoảng để phá trị tuyệt đối.

- Sử dụng phương pháp tính tích phân hàm hữu tỉ khi bậc tử > bậc mẫu (chia tử cho mẫu).

- Sử dụng các nguyên hàm cơ bản để tính tích phân.

Lời giải chi tiết:

Ta có: \(\dfrac{{{x^2} - x - 2}}{{x - 1}} = \dfrac{{\left( {x + 1} \right)\left( {x - 2} \right)}}{{x - 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 2\end{array} \right.\).

Ta có bảng xét dấu:

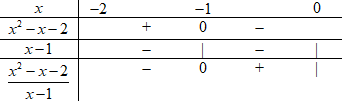
Khi đó ta có:

\(\begin{array}{l}I = \int\limits_{ - 2}^0 {\left| {\dfrac{{{x^2} - x - 2}}{{x - 1}}} \right|dx} \\\,\,\,\, = \int\limits_{ - 2}^{ - 1} {\left| {\dfrac{{{x^2} - x - 2}}{{x - 1}}} \right|dx}  + \int\limits_{ - 1}^0 {\left| {\dfrac{{{x^2} - x - 2}}{{x - 1}}} \right|dx} \\\,\,\,\, =  - \int\limits_{ - 2}^{ - 1} {\dfrac{{{x^2} - x - 2}}{{x - 1}}dx}  + \int\limits_{ - 1}^0 {\dfrac{{{x^2} - x - 2}}{{x - 1}}dx} \\\,\,\,\, =  - \int\limits_{ - 2}^{ - 1} {\left( {x - \dfrac{2}{{x - 1}}} \right)dx}  + \int\limits_{ - 1}^0 {\left( {x - \dfrac{2}{{x - 1}}} \right)dx} \\\,\,\,\, =  - \left. {\left( {\dfrac{{{x^2}}}{2} - 2\ln \left| {x - 1} \right|} \right)} \right|_{ - 2}^{ - 1} + \left. {\left( {\dfrac{{{x^2}}}{2} - 2\ln \left| {x - 1} \right|} \right)} \right|_{ - 1}^0\\\,\,\,\, =  - \left( {\dfrac{1}{2} - 2\ln 2} \right) + \left( {2 - 2\ln 3} \right) - \left( {\dfrac{1}{2} - 2\ln 2} \right)\\\,\,\,\, = 1 + 4\ln 2 - 2\ln 3\\ \Rightarrow a = 1,\,\,b = 4,\,\,c =  - 2\end{array}\)

Vậy \(T = 2{a^3} + 3b - 4c = {2.1^3} + 3.4 - 4\left( { - 2} \right) = 22\).

Chọn C.