Câu hỏi
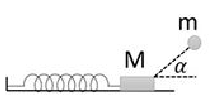
Một con lắc lò xo nằm ngang gồm lò xo có khối lượng không đáng kể, độ cứng k = 100 N/m gắn với vật có khối lượng M = 400 g. Khi M đang đứng yên tại vị trí lò xo không biến dạng thì vật m bay từ phía trên tới va chạm và dính vào M. Biết rằng va chạm giữa m và M là va chạm mềm; hệ số ma sát trượt giữa hệ vật (m + M) và mặt nằm ngang là 0,1; khối lượng m = 100 g; khi m tiếp xúc với M, vận tốc của vật m là 20 m/s và hợp với phương ngang một góc 600; lấy g = 10 m/s2. Sau va chạm, độ giãn cực đại của lò xo gần nhất với giá trị nào sau đây?
- A 26,79 cm.
- B 27,79 cm
- C 12,65 cm.
- D 13,65 cm
Phương pháp giải:
+ Áp dụng định luật bảo toàn động lượng theo phương ngang cho hai vật m và M khi va chạm :
\(m.v.\cos \alpha = (m + M).v'\)
+ Sau va chạm, hệ vật (m+M) dao động tắt dần do có ma sát, vị trí bị nén cực đại cách vị trí cân bằng A1.
Áp dụng định luật bảo toàn năng lượng ta có:
\(\frac{1}{2}.(m + M).v{'^2} = {F_{ms}}.{A_1} + \frac{1}{2}.k.A_1^2 = \mu .(m + M).g.{A_1} + \frac{1}{2}.k.A_1^2\)
Tìm được A1
+ Sau đó vật chuyển động sang trái, khi đó lò xo bị giãn đến vị trí cách vị trí cân bằng A2
Ta có:
\(\frac{1}{2}.k.A_1^2 - \frac{1}{2}.k.A_2^2 = \mu .(m + M).g.({A_1} + {A_2})\)
Tìm được A2 chính là độ giãn cực đại của lò xo.
Lời giải chi tiết:
Áp dụng định luật bảo toàn động lượng theo phương ngang cho hai vật m và M khi va chạm.
\(\begin{array}{l}
m.v.\cos \alpha = (m + M).v'\\
\Rightarrow v' = \frac{{m.v.\cos \alpha }}{{m + M}} = \frac{{0,1.20.\cos {{60}^0}}}{{0,1 + 0,4}} = 2\left( {m/s} \right)
\end{array}\)
Sau va chạm, hệ vật (m+M) dao động tắt dần do có ma sát, vị trí bị nén cực đại cách vị trí cân bằng A1.
Áp dụng định luật bảo toàn năng lượng ta có:
\(\begin{array}{l}
\frac{1}{2}.(m + M).v{'^2} = {F_{ms}}.{A_1} + \frac{1}{2}.k.A_1^2 = \mu .(m + M).g.{A_1} + \frac{1}{2}.k.A_1^2\\
\Rightarrow \frac{1}{2}.0,{5.2^2} = 0,1.0,5.10.{A_1} + 50.A_1^2\\
\Rightarrow {A_1} = 0,{1365_{}}m = 13,{65_{}}cm
\end{array}\)
Sau đó vật chuyển động sang trái, khi đó lò xo bị giãn đến vị trí cách vị trí cân bằng A2
Ta có:
\(\begin{array}{l}
\frac{1}{2}.k.A_1^2 - \frac{1}{2}.k.A_2^2 = \mu .(m + M).g.({A_1} + {A_2})\\
\Rightarrow \frac{1}{2}.k.({A_1} - {A_2}) = \mu .(m + M).g \Rightarrow 50.({A_1} - {A_2}) = 0,1.0,5.10\\
\Rightarrow {A_1} - {A_2} = 0,01m = 1cm \Rightarrow {A_2} = {A_1} - 1 = 13,65 - 1 = 12,65cm
\end{array}\)
Tìm được A2 = 12,65cm chính là độ giãn cực đại của lò xo.
Chọn C.