Câu hỏi
Một con lắc lò xo dao động điều hòa trên trục Ox nằm ngang. Trong quá trình dao động, chiều dài lớn nhất và nhỏ nhất của lò xo là 90cm và 80cm. Gia tốc a (m/s2) và li độ x (m) của con lắc tại cùng một thời điểm liên hệ với nhau qua hệ thức \(x = - 0,025a\). Tại thời điểm t = 0,25s vật ở li độ \(x = - 2,5\sqrt 3 cm\)và đang chuyển động theo chiều dương, lấy \({\pi ^2} = 10\) phương trình dao động của con lắc là:
- A \(x = 5\sqrt 2 .\cos \left( {2\pi t - \dfrac{{5\pi }}{6}} \right)\left( {cm} \right)\)
- B \(x = 5.\cos \left( {\pi t - \dfrac{{5\pi }}{6}} \right)\left( {cm} \right)\)
- C \(x = 5.\cos \left( {2\pi t - \dfrac{{4\pi }}{3}} \right)\left( {cm} \right)\)
- D \(x = 5\sqrt 2 .\cos \left( {\pi t - \dfrac{{4\pi }}{3}} \right)\left( {cm} \right)\)
Phương pháp giải:
Biên độ dao động: \(A = \dfrac{{{l_{\max }} - {l_{\min }}}}{2}\)
Hệ thức liên hệ giữa a và x: \(a = - {\omega ^2}x \Rightarrow \omega \)
Dựa vào dữ kiện: “Tại thời điểm t = 0,2s vật ở li độ \(x = - 2,5\sqrt 3 cm\)và đang chuyển động theo chiều dương” xác định được pha ban đầu φ.
Lời giải chi tiết:
Biên độ dao động: \(A = \dfrac{{{l_{\max }} - {l_{\min }}}}{2} = \dfrac{{90 - 80}}{2} = 5cm\)
Ta có:
\(\begin{array}{l}x = - 0,025a \Rightarrow a = - \dfrac{1}{{0,025}}.x \Rightarrow {\omega ^2} = \dfrac{1}{{0,025}} = 40\\ \Rightarrow \omega = 2\sqrt {10} = 2\pi \,\left( {rad/s} \right)\end{array}\)
Tại thời điểm t = 0,25s vật ở li độ \(x = - 2,5\sqrt 3 cm\)và đang chuyển động theo chiều dương. Biểu diễn trên VTLG ta có:
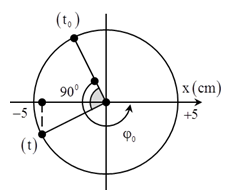
Từ VTLG ta có:
\(\omega t + \varphi = 2\pi .0,25 + \varphi = - \dfrac{{5\pi }}{6} \Rightarrow \varphi = - \dfrac{{4\pi }}{3}\)
Phương trình dao động: \(x = 5.\cos \left( {2\pi t - \dfrac{{4\pi }}{3}} \right)\left( {cm} \right)\)
Chọn C.







