Câu hỏi
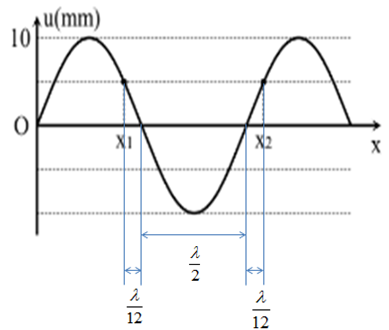
Một sóng hình sin lan truyền trên trục Ox. Hinh dạng sóng tại một thời điểm t nào đó như hình vẽ. Biết \({x_2} - {x_1} = 10cm\). Gọi \(\delta \) là tỉ số cực đại của tốc độ dao động và tốc độ truyền sóng. Giá trị của \(\delta \) gần nhất với đáp án nào nhất sau đây?
- A \(4,0.\)
- B \(0,2.\)
- C \(0,4.\)
- D \(2,0.\)
Phương pháp giải:
+ Sử dụng biểu thức tính vận tốc cực đại: \({v_{max}} = A\omega \)
+ Sử dụng biểu thức tính tốc độ truyền sóng: \(v = \lambda f\)
Lời giải chi tiết:
Ta có: \(\delta = \dfrac{{{v_{max}}}}{v} = \dfrac{{2\pi f.A}}{{\lambda f}} = 2\pi \dfrac{A}{\lambda }\)
Từ đồ thị, ta có:
+ Biên độ \(A = 10mm = 1cm\)
\(\begin{array}{l}{x_2} - {x_1} = 2\dfrac{\lambda }{{12}} + \dfrac{\lambda }{2} = \dfrac{{2\lambda }}{3} = 10cm\\ \Rightarrow \lambda = 15cm\end{array}\)
\( \Rightarrow \delta = 2\pi \dfrac{A}{\lambda } = \dfrac{{2\pi .1}}{{15}} = 0,4188\)
Chọn D
Câu hỏi trước
