Câu hỏi
Bạn Bình muốn làm một chiếc thùng hình trụ không đáy từ nguyên liệu là mảnh tôn hình tam giác đều \(ABC\) có cạnh bằng \(60\left( {cm} \right)\). Bạn muốn cắt mảnh tôn hình chữ nhật \(MNPQ\) từ mảnh tôn nguyên liệu (với \(M,N\) thuộc cạnh \(BC\); \(P,Q\) tương ứng thuộc cạnh \(AC\) và \(AB\)) để tạo thành hình trụ có chiều cao bằng \(MQ\). Thể tích lớn nhất của chiếc thùng mà bạn Bình có thể làm được là:
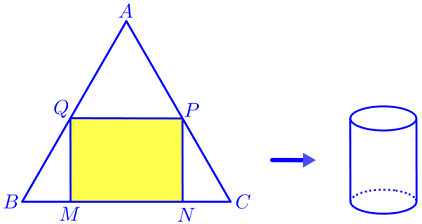
- A \(\dfrac{{8000\sqrt 3 }}{\pi }\left( {c{m^3}} \right)\)
- B \(\dfrac{{6825}}{{4\pi }}\left( {c{m^3}} \right)\)
- C \(\dfrac{{6825}}{{2\pi }}\left( {c{m^3}} \right)\)
- D \(\dfrac{{4000\sqrt 3 }}{\pi }\left( {c{m^3}} \right)\)
Phương pháp giải:
- Đưa độ dài cạnh hình chữ nhật \(MNPQ\) về cùng một biến và tìm điều kiện của biến.
- Hình trụ tạo thành có chiều cao bằng \(MQ\) và chu vi đáy bằng \(MN\).
- Tính thể tích của hình trụ theo biến.
- Bài toán trở thành tìm giá trị lớn nhất của hàm số.
Lời giải chi tiết:
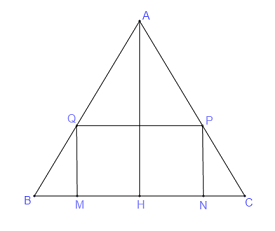
Gọi \(H\) là trung điểm của \(BC\) \( \Rightarrow H\) cũng là trung điểm của \(MN\).
Do \(ABC\) là tam giác đều có cạnh bằng \(60\,\,\left( {cm} \right)\) nên \(\left\{ \begin{array}{l}AH \bot BC\\BH = HC = 30\left( {cm} \right)\\AH = \dfrac{{\sqrt 3 }}{2}.BC = 30\sqrt 3 \left( {cm} \right)\end{array} \right.\)
Đặt \(BM = x\), do \(BM < BH \Rightarrow 0 < x < 30\), ta có :
\(\begin{array}{l}MH = BH - BM = 30 - x\\ \Rightarrow MN = 2MH = 60 - 2x\end{array}\)
\(\left\{ \begin{array}{l}AH \bot BC\\QM \bot MN \Rightarrow QM \bot BC\end{array} \right. \Rightarrow AH\parallel QM\)
\( \Rightarrow \dfrac{{QM}}{{AH}} = \dfrac{{BM}}{{BH}} \Leftrightarrow \dfrac{{QM}}{{30\sqrt 3 }} = \dfrac{x}{{30}}\)\( \Leftrightarrow QM = \sqrt 3 x\) (Định lí Ta-lét)
Gọi \(r\) là bán kính đáy của hình trụ được tạo thành.
Hình trụ được tạo thành có chiều cao bằng \(MQ = \sqrt 3 x\) và chu vi đáy bằng \(MN\) nên :
\(2\pi r = MN \Leftrightarrow 2\pi r = 60 - 2x \Leftrightarrow r = \dfrac{{30 - x}}{\pi }\)
Thể tích của hình trụ được tạo thành từ hình chữ nhật \(MNPQ\) là :
\(\begin{array}{l}V = \pi {r^2}.MQ = \pi .{\left( {\dfrac{{30 - x}}{\pi }} \right)^2}.\sqrt 3 x\\\,\,\,\,\, = \dfrac{{\sqrt 3 x\left( {900 - 60x + {x^2}} \right)}}{\pi }\\\,\,\,\,\, = \dfrac{{\sqrt 3 }}{\pi }\left( {{x^3} - 60{x^2} + 900x} \right)\end{array}\)
Xét hàm số \(f\left( x \right) = {x^3} - 60{x^2} + 900x\) trên khoảng \(\left( {0;30} \right)\) ta có :
\(\begin{array}{l}f'\left( x \right) = 3{x^2} - 120x + 900\\f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 30\,\,\left( {ktm} \right)\\x = 10\,\,\,\left( {tm} \right)\end{array} \right. \Leftrightarrow x = 10\end{array}\)
Ta có BBT như sau :
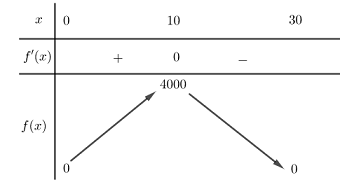
Từ BBT ta thấy \(\mathop {\max }\limits_{\left( {0;30} \right)} f\left( x \right) = f\left( {10} \right) = 4000\).
Do đó, thể tích lớn nhất của hình trụ tạo được là \(\dfrac{{4000\sqrt 3 }}{\pi }\,\,\,\left( {c{m^3}} \right).\)
Chọn D.







