Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} - 4} \right)\left( {2 - x} \right)\left( {6 - x} \right)\). Mệnh đề nào sau đây đúng?
- A \(f\left( 1 \right) < f\left( { - 2} \right) < f\left( 0 \right)\)
- B \(f\left( { - 2} \right) < f\left( 1 \right) < f\left( 0 \right)\)
- C \(f\left( 1 \right) < f\left( 0 \right) < f\left( { - 2} \right)\)
- D \(f\left( { - 2} \right) < f\left( 0 \right) < f\left( 1 \right)\)
Phương pháp giải:
Lập bảng biến thiên, rồi đưa ra đánh giá.
Lời giải chi tiết:
\(\begin{array}{l}f'\left( x \right) = \left( {{x^2} - 4} \right)\left( {2 - x} \right)\left( {6 - x} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = {\left( {x - 2} \right)^2}\left( {x + 2} \right)\left( {x - 6} \right)\\f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\\x = 6\end{array} \right.\end{array}\)
Bảng biến thiên:
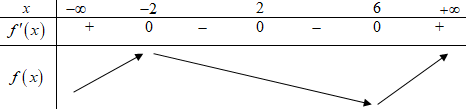
Dựa vào BBT, ta có \(f\left( 1 \right) < f\left( 0 \right) < f\left( { - 2} \right)\).
Chọn: C.
Câu hỏi trước
