Câu hỏi
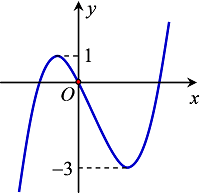
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình bên. Tất cả các giá trị của tham số m để hàm số \(y = \left| {f\left( x \right) + m} \right|\) có ba điểm cực trị là:
- A \(1 \le m \le 3\).
- B \(m \le - 3\) hoặc \(m \ge 1\).
- C \(m \le - 1\) hoặc \(m \ge 3\).
- D \(m = - 1\) hoặc \(m = 3\).
Phương pháp giải:
Cho \(\left( C \right)\) là đồ thị của hàm số \(y = f\left( x \right)\) và \(p > 0\):
+) Tịnh tiến \(\left( C \right)\) lên trên \(p\) đơn vị thì được đồ thị \(y = f\left( x \right) + p.\)
+) Tịnh tiến \(\left( C \right)\) xuống dưới \(p\) đơn vị thì được đồ thị \(y = f\left( x \right) - p.\)
Lời giải chi tiết:
Để hàm số \(y = \left| {f\left( x \right) + m} \right|\) có ba điểm cực trị thì \(m \le - 1\) hoặc \(m \ge 3\).
Tức là: Tịnh tiến đồ thị \(y = f\left( x \right)\) lên trên \(m\) đơn vị, với \(m \ge 3\); hoặc tịnh tiến đồ thị \(y = f\left( x \right)\) xuống dưới \(\left( { - m} \right)\) đơn vị, với \(m \le - 1\).
Chọn: C.
Câu hỏi trước
