Lời giải chi tiết:

Ta có: \(y = \left| {x + 1} \right| - x + m = \left[ \begin{array}{l}1 + m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge  - 1\\ - 2x - 1 + m\,\,\,khi\,\,x < 1\end{array} \right.\)

Xét phương trình hoành độ giao điểm :

      \(\dfrac{x}{{x + 1}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{x + 2}}{{x + 3}} = 1 + m\,\,\left( {x >  - 1} \right)\)            (1)  , 

      \(\dfrac{x}{{x + 1}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{x + 2}}{{x + 3}} =  - 2x - 1 + m\,\,\,\left( {x <  - 1} \right)\)  (2)

*) Xét phương trình (1) :

\(y = f\left( x \right) = \dfrac{x}{{x + 1}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{x + 2}}{{x + 3}}\)\( \Rightarrow y' = \dfrac{1}{{{{\left( {x + 1} \right)}^2}}} + \dfrac{1}{{{{\left( {x + 2} \right)}^2}}} + \dfrac{1}{{{{\left( {x + 3} \right)}^3}}} > 0,\forall x >  - 1\)

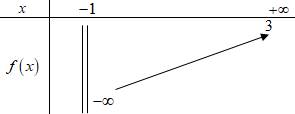
Như vậy, với \(m + 1 \ge 3 \Leftrightarrow m \ge 2:\,\,\)(1) vô nghiệm, 

                với \(m + 1 < 3 \Leftrightarrow m < 2:\,\,\,\left( 1 \right)\) có nghiệm duy nhất \({x_0}\,\,\left( {{x_0} >  - 1} \right)\).

*) Xét phương trình \(\left( 2 \right) \Leftrightarrow \dfrac{x}{{x + 1}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{x + 2}}{{x + 3}} + 2x =  - 1 + m\,\,\,\left( {x <  - 1} \right)\)

\(y = g\left( x \right) = \dfrac{x}{{x + 1}} + \dfrac{{x + 1}}{{x + 2}} + \dfrac{{x + 2}}{{x + 3}} + 2x \Rightarrow y' = \dfrac{1}{{{{\left( {x + 1} \right)}^2}}} + \dfrac{1}{{{{\left( {x + 2} \right)}^2}}} + \dfrac{1}{{{{\left( {x + 3} \right)}^3}}} + 2 > 0,\) với \(\forall x \in \mathbb{R}\backslash \left\{ { - 2; - 3} \right\}\)

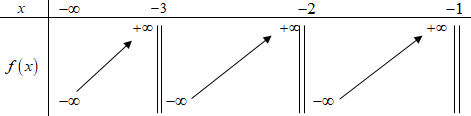
Như vậy, với mọi giá trị của m thì (2) luôn có 3 nghiệm phân biệt \({x_1},{x_2},{x_3}\,\,\left( {{x_1} <  - 3,\,\, - 3 < {x_2} <  - 2,\,\, - 2 < {x_3} <  - 1} \right)\)

Vậy, để \(\left( {{C_1}} \right)\) cắt \(\left( {{C_2}} \right)\) tại 3 điểm phân biệt thì \(m \ge 2\).

Chọn C.