Phương pháp giải:

- Đặt ẩn phụ \(t = \sin x\,\,\left( {t \in \left[ {0;1} \right]} \right)\).

- Lập BBT của hàm số và kết luận GTLN của hàm số.

- Đồng nhất hệ số, tìm \(a,\,\,b,\,\,c,\,\,d\) và tính tổng \(a + b + c + d\).

Lời giải chi tiết:

Ta có: \(y = {\cos ^2}x.{e^{\sin x}} = \left( {1 - {{\sin }^2}x} \right).{e^{\sin x}}\).

Đặt \(\sin x = t\,\,\,\left( {0 \le t \le 1} \right)\) ta có: \(y = \left( {1 - {t^2}} \right).{e^t}\).

\(\begin{array}{l} \Rightarrow y' = \left( { - 2t} \right).{e^t} + \left( {1 - {t^2}} \right){e^t} = {e^t}.\left( {1 - 2t - {t^2}} \right)\\\,\,\,\,\,\,y' = 0 \Rightarrow \left[ \begin{array}{l}t =  - 1 - \sqrt 2  \notin \left[ {0;1} \right]\\t =  - 1 + \sqrt 2  \in \left[ {0;1} \right]\end{array} \right.\end{array}\)

Bảng biến thiên:

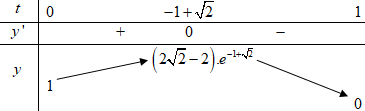
Vậy \(\left\{ \begin{array}{l}a = 2\\b =  - 2\\c = 1\\d =  - 1\end{array} \right. \Rightarrow a + b + c + d = 2 - 2 + 1 - 1 = 0.\)

Chọn C.