Lời giải chi tiết:

\(\begin{array}{l}\,\,\,\,\,\,f\left( x \right) \ge 0\,\,\,\forall x \in \left[ {2;4} \right]\\ \Leftrightarrow 8{x^3} - 36{x^2} + 53x - 25 - m - \sqrt[3]{{3x - 5 + m}} \ge 0\,\,\,\forall x \in \left[ {2;4} \right]\\ \Leftrightarrow \left( {8{x^3} - 36{x^2} + 54x - 27} \right) + 2x - 3 - \left( {3x + m - 5 + \sqrt[3]{{3x + m - 5}}} \right) \ge 0\,\,\,\forall x \in \left[ {2;4} \right]\\ \Leftrightarrow {\left( {2x - 3} \right)^3} + 2x - 3 - \left( {3x + m - 5} \right) - \sqrt[3]{{3x + m - 5}} \ge 0\,\,\,\forall x \in \left[ {2;4} \right]\\ \Leftrightarrow \left[ {{{\left( {2x - 3} \right)}^3} - \left( {3x + m - 5} \right)} \right] + \left( {2x - 3 - \sqrt[3]{{3x + m - 5}}} \right) \ge 0\,\,\,\forall x \in \left[ {2;4} \right]\\ \Leftrightarrow \left( {2x - 3 - \sqrt[3]{{3x + m - 5}}} \right)\left( {{{\left( {2x - 3} \right)}^2} + \left( {2x - 3} \right)\sqrt[3]{{3x + m - 5}} + \sqrt[3]{{{{\left( {3x + m - 5} \right)}^2}}} + 1} \right) \ge 0\,\,\,\forall x \in \left[ {2;4} \right]\\ \Leftrightarrow 2x - 3 - \sqrt[3]{{3x + m - 5}} \ge 0\,\,\,\forall x \in \left[ {2;4} \right]\\\left( {do\,\,{{\left( {2x - 3} \right)}^2} + \left( {2x - 3} \right)\sqrt[3]{{3x + m - 5}} + \sqrt[3]{{{{\left( {3x + m - 5} \right)}^2}}} + 1 > 0\,\,\forall x} \right)\\ \Leftrightarrow \sqrt[3]{{3x + m - 5}} \le 2x - 3\,\,\,\forall x \in \left[ {2;4} \right]\\ \Leftrightarrow 3x + m - 5 \le 8{x^3} - 36{x^2} + 54x - 27\,\,\,\forall x \in \left[ {2;4} \right]\\ \Leftrightarrow m \le 8{x^3} - 36{x^2} + 51x - 22\,\,\,\forall x \in \left[ {2;4} \right]\\ \Leftrightarrow m \le \mathop {\min }\limits_{\left[ {2;4} \right]} \left( {8{x^3} - 36{x^2} + 51x - 22} \right)\end{array}\)

Đặt \(g\left( x \right) = 8{x^3} - 36{x^2} + 51x - 22\) ta có: \(g'\left( x \right) = 24{x^2} - 72x + 51\).

Cho \(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{6 + \sqrt 2 }}{4}\\x = \dfrac{{6 - \sqrt 2 }}{4}\end{array} \right.\).

Bảng biến thiên:

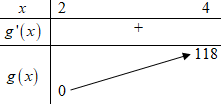
Dựa vào BBT ta thấy \(\mathop {\min }\limits_{\left[ {2;4} \right]} g\left( x \right) = 0 \Leftrightarrow m \le 0\).

Kết hợp điều kiện đề bài ta có \(m \in \left[ { - 2019;0} \right],\,\,m \in \mathbb{Z}\)\( \Rightarrow m \in \left\{ { - 2019; - 2018;...;0} \right\}\).

Vậy có \(2020\) giá trị của \(m\) thỏa mãn yêu cầu bài toán.

Chọn A.