Phương pháp giải:

- Hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) tiếp xúc với nhau khi và chỉ khi hệ phương trình \(\left\{ \begin{array}{l}f\left( x \right) = g\left( x \right)\\f'\left( x \right) = g'\left( x \right)\end{array} \right.\) có nghiệm.

- Rút \(a,\,\,b\) theo \(x\). Đặt \(a + b = f\left( x \right)\).

- Sử dụng phương pháp hàm số tìm GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {0;3} \right]\).

Lời giải chi tiết:

Hoành độ tiếp điểm của hai đồ thị hàm số thỏa mãn hệ phương trình:

\(\begin{array}{l}\,\,\,\,\,\,\left\{ \begin{array}{l} - {x^3} + 3x - 1 = ax + b\\ - 3{x^2} + 3 = a\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 3{x^2} + 3 = a\\ - {x^3} + 3x - 1 = x\left( { - 3{x^2} + 3} \right) + b\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a =  - 3{x^2} + 3\\b = 2{x^3} - 1\end{array} \right.\end{array}\)

Khi đó ta có: \(a + b = 2{x^3} - 3{x^2} + 2\).

Đặt \(f\left( x \right) = 2{x^3} - 3{x^2} + 2\), với \(x \in \left[ {0;3} \right]\) ta có:

\(f'\left( x \right) = 6{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\).

Bảng biến thiên:

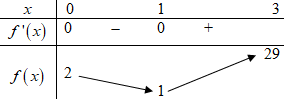
Vậy giá trị nhỏ nhất của biểu thức \(S = a + b\)bằng 1.

Chọn A.