Phương pháp giải:

Áp dụng điều kiện xác định của hàm logarit

Lời giải chi tiết:

Hàm số \(y = \ln \left( {3 - \sqrt {{x^2} - 2x + m - 2} } \right)\) xác định trên \(\left[ {0;3} \right]\) khi và chỉ khi:

\(\left\{ \begin{array}{l}{x^2} - 2x + m - 2 \ge 0\\3 - \sqrt {{x^2} - 2x + m - 2}  > 0\end{array} \right.\,\,\,\,\forall x \in \left[ {0;3} \right]\)\(\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}{x^2} - 2x + m - 2 \ge 0\\\sqrt {{x^2} - 2x + m - 2}  < 3\end{array} \right.\,\,\,\forall x \in \left[ {0;3} \right]\\ \Rightarrow \left\{ \begin{array}{l}{x^2} - 2x + m - 2 \ge 0\\{x^2} - 2x + m - 2 < 9\end{array} \right.\,\,\,\,\,\,\forall x \in \left[ {0;3} \right]\\ \Rightarrow \left\{ \begin{array}{l}m + 9 \ge  - {x^2} + 2x + 11\,\,\,\left( 1 \right)\\m <  - {x^2} + 2x + 11\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\,\,\,\,\,\,\,\,\,\forall x \in \left[ {0;3} \right]\end{array}\)

Xét hàm số \(g\left( x \right) =  - {x^2} + 2x + 11\) trên \(\left[ {0;3} \right]\) ta có:

\(g'\left( x \right) =  - 2x + 2 = 0 \Leftrightarrow x = 1\).

Bảng biến thiên:

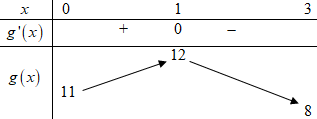
\(\left( 1 \right) \Leftrightarrow m + 9 \ge \mathop {\max }\limits_{\left[ {0;3} \right]} g\left( x \right) = 12 \Leftrightarrow m \ge 3\).

\(\left( 2 \right) \Leftrightarrow m < \mathop {\min }\limits_{\left[ {0;3} \right]} g\left( x \right) \Leftrightarrow m < 8\).

Vậy \(3 \le m < 8\), mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {3;4;5;6;7} \right\}\).

Vậy có 5 giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.

Chọn C.